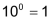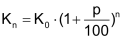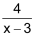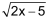Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Abschreibung
|
Ein Gerät oder Fahrzeug verliert jedes Jahr an Wert. In der Buchhaltung ist es üblich, diesen Wertverlust pro Jahr mit einem konstanten Prozentsatz zu verbuchen. Man nennt dies «Abschreibung». Mathematisch gesehen ist die Abschreibung eine exponentielle Abnahme des (Buch-)Werts. |
| siehe auch radioaktiver Zerfall |
absolute Häufigkeit
|
siehe Häufigkeit |
absoluter Fehler
|
Bei einem Messresultat ohne Fehlerangabe gilt die letzte Stelle als gerundet: |
| Günstig ist die Angabe des Messresultats mit dem absoluten Fehler: (64,3 ± 0,2) mm. |
| siehe relativer Fehler und gültige Ziffern |
Abstand
| • | Der Abstand zweier Punkte P und Q ist die Länge der kürzesten Verbindung zwischen ihnen. Man spricht auch von der «Distanz», der «Entfernung» der beiden Punkte oder von der «Länge der Strecke» von P nach Q. |
| • | Der Abstand zwischen einem Punkt und einer Geraden ist die Länge des Lots vom Punkt auf die Gerade. |
| • | Der Abstand zweier Parallelen ist die Länge eines gemeinsamen Lots. (vgl. auch Streifenbreite). |
Achse
| Der Ausdruck wird in verschiedenen Zusammenhängen gebraucht: | |
| 1 | Im (ebenen) Koordinatensystem teilen x- und y-Achse die Ebene in vier Teilgebiete ein, sodass die Lage jedes Punktes durch zwei Zahlen festgelegt ist (siehe Koordinaten). |
| 2 |
Bei einer Geradenspiegelung in der Ebene oder bei der Symmetrieachse einer Figur spricht man kurz von «Achse» (siehe Achsenspiegelung). |
| 3 |
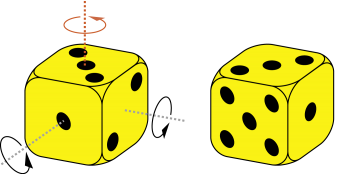
Die Drehung eines Objektes im Raum wird festgelegt durch eine Drehachse und den zugehörigen Drehwinkel. Wird zum Beispiel der linke Würfel in der Abbildung unten um 90° um die vertikale Achse gedreht, ergibt sich die Lage, wie sie in der Abbildung rechts wiedergegeben ist. |
 |
|
Achsenspiegelung
 |
||
| 1 | Die Achsenspiegelung ist eine Kongruenzabbildung. | |
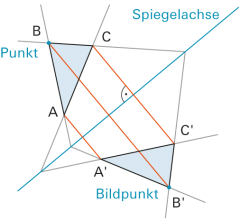
| • | Die Spiegelachse ist Mittelsenkrechte der Verbindungsstrecke zwischen Punkt und Bildpunkt. | |
| • | Original- und Bildgerade schneiden sich auf der Spiegelachse. | |
| • | Das Bild einer Achsen-Parallelen ist wieder parallel zur Achse | |
| Wird ein ebenes Vieleck an einer Geraden (Spiegelachse) gespiegelt, so hat das Bild den entgegengesetzten Drehsinn. Man spricht hier auch von «entgegengesetzter Orientierung». | ||
| Die Achsenspiegelung wird auch «Geradenspiegelung» genannt. | ||
 |
||
| 2 | Eine Figur heisst achsensymmetrisch, wenn sie beim Falten längs einer bestimmten Geraden mit sich zur Deckung gebracht werden kann. Diese Achse heisst «Symmetrieachse» oder «Spiegelachse». | |
| Eine achsensymmetrische Figur kann auch durch Spiegeln erzeugt werden. | ||
Achsensymmetrie
|
siehe Achsenspiegelung |
Achsentrapez
Addition
|
Die Addition ist eine Operation erster Ordnung. |
||
|
Eine Summe ist … |
||
| a) | das Ergebnis einer Addition: | |
| 15 + 8 = 23 2a + 3a = 5a | ||
| oder | ||
| b) | der (nicht ausgerechnete) Term mit dem Pluszeichen als Hauptzeichen: | |
 |
||
|
Für die Addition gelten das Assoziativ- und das Kommutativ-Gesetz. |
||
|
Die Umkehroperation der Addition ist die Subtraktion. |
||
| 12 + 7 = 19 ⇔ 19 - 7 = 12 | ||
| Siehe auch Rechengesetze und Bruchoperationen |
Additionsverfahren
| Verfahren zur algebraischen Lösung eines linearen Gleichungssystemes. | |
| Gegeben seien zwei Gleichungen: | 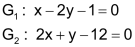 |
| Schritt 1 Gleichung G2 so umformen, dass bei der Addition G1 ⊕ G2 das y «wegfällt» (im Beispiel durch Multiplikation mit 2). |
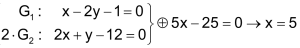 |
| Schritt 2 Ergebnis in Gleichung G1 einsetzen. |
|
|
siehe auch Einsetzungsverfahren und Gleichsetzungsverfahren |
|
ähnlich
Mathematisches Zeichen dafür ist die Wellenlinie: A ∼ B. |
| Ähnliche Figuren kann man durch zentrische Streckung erzeugen. |
Ähnlichkeitsabbildung
|
Haben bei einer Abbildung Original und Bildfigur die gleiche Form, so spricht man von «Ähnlichkeitsabbildung». |
|
Beispiel: |
| Ein Kopierer führt beim Vergrössern oder Verkleinern eine Ähnlichkeitsabbildung aus. |
|
Wichtigste Ähnlichkeitsabbildung ist die Zentrische Streckung. |
Algorithmus
| Ein Algorithmus ist eine Folge von Anweisungen, nach der eine Berechnung ausgeführt oder eine Ordnung hergestellt wird. Man könnte auch von einer «Programmiervorschrift» reden, die es erlaubt, einen Prozess an eine Maschine auszulagern. | |
| Beispiele | |
|
♦ ♦ ♦ ♦ |
die schriftlichen Rechenverfahren ggT-Bestimmung Heron-Verfahren zur Bestimmung der Quadratwurzel einer Zahl Sortieren einer Namensliste nach Alphabet oder von Zahlen nach ihrer Grösse |
allgemeingültig
|
Wird eine Gleichung oder eine Ungleichung (jeweils mit einer Unbekannten) durch jede Zahl erfüllt, so spricht man von einer «allgemeingültigen Gleichung» bzw. von einer «allgemeingültigen Ungleichung». |
|
Beispiel
|
Altersquotient
|
Der Altersquotient ist definiert als Verhältnis |
 |
| der Wohnbevölkerung. |
äquivalent
| siehe gleichwertig |
Äquivalenzumformung
| Eine Operation, welche eine Gleichung in eine andere Gleichung mit denselben Lösungen überführt, heisst «Äquivalenzumformung» – die beiden Gleichungen nennt man auch «äquivalent». | |
| Äquivalenzumformungen sind … | |
| • | auf beiden Seiten der Gleichung denselben Term addieren oder subtrahieren |
| • | beide Seiten der Gleichung mit demselben Term multiplizieren oder durch denselben Term dividieren, wobei der Term die Unbekannte nicht enthalten darf |
| • | ordnen und zusammenfassen auf der einen oder andern Seite des Gleichheitszeichens |
archimedische Körper
|
Archimedische Körper sind Polyeder, deren Oberfläche sich aus zwei oder mehr verschiedenen Typen regelmässiger Vielecke zusammensetzt. Dabei muss an jeder Ecke die gleiche Konfiguration vorhanden sein. |
|
Zwei Beispiele |
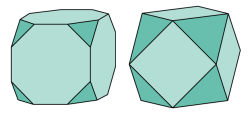 |
| siehe auch platonische Körper |
archimedisches Parkett
| Siehe reguläres Parkett |
arithmetisches Mittel
|
Das arithmetisches Mittel von n Werten wird wie folgt berechnet: |
|
|
Beispiel Das arithmetische Mittel beträgt |
|
|
Oft spricht man auch einfach von «Durchschnitt». |
|
| siehe auch Median und geometrisches Mittel |
Assoziativgesetz
| Siehe Rechengesetze |
ausklammern
| Eine Technik zum Faktorisieren von Summen: Steckt in allen Summanden der Summe ein gemeinsamer Faktor, so lässt sich die Summe als Produkt schreiben. |
|
| Beispiel | |
| 12ab² – 2bc + 6ab³c = 2b · (6ab – c + 3ab²c) | |
ausmultiplizieren
|
Aus einem Produkt gemäss Distributivgesetz eine Summe herstellen. Der umgekehrte Vorgang heisst Ausklammern. |
| Siehe faktorisieren |
Balkendiagramm
| Balkendiagramme werden oft zur Darstellung von relativen oder absoluten Häufigkeiten eingesetzt. Die Anteile werden durch stehende, manchmal auch durch liegende Balken dargestellt. |
|
Beispiel 1: «relative Häufigkeit» |
|
Prozentualer Anteil an Haushalten mit 1, 2, 3, 4 oder 5 Personen |
 |
|
Beispiel 2: «absolute Häufigkeit» |
|
Anzahl Anhänger von blau, rot oder grün, welche die Kandidatinnen A bis D gewählt haben |
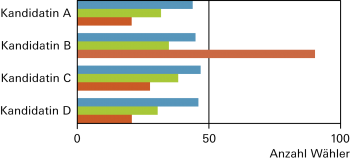 |
| Ein Diagramm wie in Beispiel 1 wird oft auch «Säulendiagramm», «Stabdiagramm» oder «Histogramm» genannt. |
Baumdiagramm
| Mehrstufige Prozesse können durch ein Baumdiagramm veranschaulicht werden. |
| Beispiel: |
| Alle möglichen Wege von Ort A nach C über Ort B. |
|
|
| Speziell wichtig sind Baumdiagramme als Hilfsmittel beim Berechnen von Wahrscheinlichkeiten und in der Kombinatorik. |
| Beispiel: |
|
Verteilung von Knaben und Mädchen in einer Familie mit drei Kindern (Geburtenfolge). |
 |
|
Es sind 8 Fälle möglich. Wenn es bei der Berechnung der Wahrscheinlichkeit um die Anzahl Mädchen geht, dann sind bloss noch 4 verschiedene Fälle zu unterscheiden: 0, 1, 2 oder 3 Mädchen. |
| Siehe auch Wahrscheinlichkeitsbaum |
Bildfigur
|
Bei einer Abbildung (z.B. einer Spiegelung) werden Figuren in ihrer Lage verändert – manchmal auch in ihrer Grösse und Form. |
|
Die Ausgangsfigur nennt man «Original», die resultierende Figur heisst «Bild» oder «Bildfigur». |
Binärsystem
|
Das Binärsystem wird auch «Dualsystem» oder «Zweiersystem» genannt. Im Zehnersystem stellen wir jede noch so grosse Zahl mit zehn verschiedenen Ziffern dar. Dualzahlen werden im Informatikbereich eingesetzt, weil ein System oft durch zwei Zustände – nämlich «1» (ein) oder «0» (aus) – beschrieben werden kann. |
|
An die Stelle der Zehnerpotenzen treten die Zweierpotenzen als Stufenzahlen: |
|
Bei der Addition zweier Zahlen werden nicht die Zehner, sondern die Zweier übertragen: |
binomische Formeln
|
Eine wichtige Rolle beim Faktorisieren von Summen haben die drei Binomischen Formeln. Ihre Bedeutung geht aber weit über dies hinaus. Der Name deutet auf zweiteilige Summen (lateinisch «bi» für «zweimal»). |
|
| Formel 1 (a + b)2 = a2 + 2ab + b2 | |
| geometrische Deutung: | |
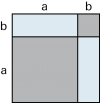 |
|
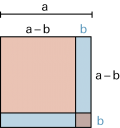
| Formel 2 (a – b)2 = a2 – 2ab + b2 | |
| geometrische Deutung: | |
 |
|
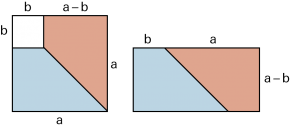
| Formel 3 (a + b) ∙ (a – b) = a2 – b2 | |
| geometrische Deutung: | |
 |
|
Bit - Byte
| Ein Bit ist die kleinstmögliche Informationsmenge, die man auf einem Computer speichern kann. Man kann sich darunter eine Schalterstellung «an» oder «aus», «ja» oder «nein» beziehungsweise «1» oder «0» vorstellen. |
|
8 Bit werden zu 1 Byte gebündelt. 1 Byte ist also eine achtkomponentige Informationsmenge: |
| Speicherkapazitäten eines Sticks, einer Festplatte oder die Grösse eines gespeicherten Musikstücks werden in kB (Kilobyte), MB (Megabyte), GB (Gigabyte) oder TB (Terabyte) angegeben. |
Bruch
|
Ein Bruch kann als Teil eines Ganzen aufgefasst werden («Bruchteil»). |
|||
| Darstellung: | |||
 |
|||
| Der Bruchstrich kann als Divisionszeichen interpretiert werden. Wird die Division ausgeführt, wird die Zahl zum «Dezimalbruch»: | |||
 |
|||
|
Ein Bruch mit Zähler 1 heisst «Stammbruch»:
|
|||
|
Siehe auch Dezimalbruch, Prozent und Bruchoperationen |
Bruchgleichung
| Bruchgleichung ist die Bezeichnung für eine Gleichung, bei der die Unbekannte im Nenner eines Bruchs vorkommt. |
Bruchoperationen
| 1 Kürzen und Erweitern | |
|
Zu jedem Bruch gibt es weitere Brüche mit dem gleichen Wert. Man erhält sie durch kürzen und erweitern. |
|
 |
 |
| Brüche kann man durch Erweitern gleichnamig (gleich-nennrig) machen. | |
| 2 Addition und Subtraktion | |
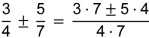 |
|
| 3 Multiplikation | |
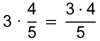 |
|
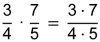 |
|
|
Beachte: |
|
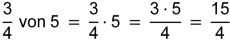 |
|
| 4 Division | |
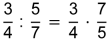 |
|
|
Regel: «Bruch 1 mal Kehrwert von Bruch 2» |
|
Cavalieri-Prinzip
| siehe Prinzip von Cavalieri |
centi-
dezi-
Dezimalbruch
|
Zahlen mit Komma oder Punkt heissen im Zehnersystem «Dezimalbruch». |
|
Beispiele für Dezimalbrüche: |
| abbrechend | 0,45 | 0,714285 |
| periodisch |
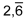 |
(gelesen: «zwei Komma Periode 6») |
| gemischt periodisch |
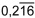 |
(gelesen: «null Komma zwei Periode eins sechs») |
|
Jeder Bruch kann auch als Dezimalbruch dargestellt werden. |
||
|
Bemerkung: |
||
|
Irrationale Zahlen können nicht als Bruch dargestellt werden. |
||
|
Beispiele: |
||
 |
||
Dezimalpunkt
|
Siehe Komma und Dezimalbruch |
Dezimalsystem
| Das Dezimalsystem ist ein Stellenwert- oder Positionssystem: Der Wert einer Ziffer hängt von ihrer Position innerhalb einer Zahl ab. Man spricht daher vom «Stellenwert» einer Ziffer. |
 |
|
Beispiel: |
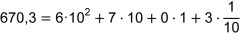 |
| Die Ziffer 6 hat in dieser Zahl den Stellenwert 6 ⋅ 102 = 600 |
| In Mesopotamien wurden Zahlen in Positionssystemen mit Basis 12 oder 60 gebraucht. Das Positionssystem mit Basis 12 hat sich bei uns in Mengenangaben wie «ein Duzend» oder «ein Gros» mit 144 (= 122) Stück gehalten; das System mit Basis 60 findet sich noch in unserer Zeiteinteilung mit 1h = 60 Minuten = 3'600 Sekunden (= 602). |
| In der Technik ist das Zweiersystem (auch «Binärsystem») von zentraler Bedeutung, weil dort mit zwei Zuständen (1 oder 0 für «Strom» oder «kein Strom») gearbeitet wird. |
| In der elektronischen Datenverarbeitung ist – neben dem Zweiersystem – ebenfalls das «Hexagesimalsystem» (Basis 16) gebräuchlich. |
| Das römische Zahlensystem ist kein Stellenwertsystem. Es eignet sich zwar zur Darstellung einer Zahl, damit zu rechnen ist aber praktisch unmöglich. |
Diagonale
Diagramm
|
Eine Darstellung, die grafisch den Zusammenhang zwischen zwei oder mehr Grössen veranschaulicht, nennen wir «Diagramm». |
|
Gebräuchliche Diagrammtypen: |
|
Von einem «Diagramm» spricht man auch, wenn die Abhängigkeit zweier Grössen in einem |
Dichte
|
Die Dichte ist definiert als Verhältnis zwischen Masse und Volumen: Die Dichte wird mit dem griechischen Buchstaben
Im Alltag sind folgende Masseinheiten gebräuchlich: |
|||
|
Beispiel |
|||
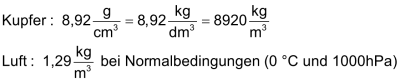 |
Differenz
|
Siehe Subtraktion |
Distributivgesetz
|
Siehe Rechengesetze |
Division
|
Die Division ist eine Operation zweiter Ordnung. |
||
|
Das Operationszeichen ist der Doppelpunkt : («durch» oder «geteilt durch», in speziellen Fällen auch «gemessen mit»); manchmal wird dafür auch ein Bruchstrich eingesetzt. |
||
|
Ein Quotient ist … |
||
| a) | das Ergebnis einer Division: | |
 |
||
| oder | ||
| b) | der (nicht ausgerechnete) Term, der von einem Durchzeichen (oder einem Bruchstrich) «zusammengehalten» wird: | |
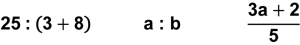 |
||
|
Die Umkehroperation der Division ist die Multiplikation. |
||
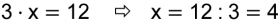 |
||
|
Damit ist eine Division durch 0 nicht erlaubt, denn dann müsste die Gleichung |
||
|
Siehe auch Bruchoperationen |
||
Doppelrechnung
| Wird eine Grösse durch Messung von mehreren Teilgrössen bestimmt – zum Beispiel eine Dichte durch Messen von Volumen und Masse – ist genau abzuklären, wie sich die Messgenauigkeiten (mögliche «Messfehler») auf das Schlussresultat auswirken. Ein praktisches Verfahren hierzu ist die «Doppelrechnung». | |
| Zuerst überlegt man sich, in welche Richtung jedes einzelne Messresultat die Schlussgrösse beeinflusst. Dann wählt man – je nachdem – den kleinstmöglichen oder den grösstmöglichen Wert der einzelnen Messresultate und setzt diese in die Formel für die Schlussgrösse ein. So erhält man eine obere und eine untere Schranke für das (Schluss-)Resultat und gleichzeitig Informationen zur Anzahl der gültigen Ziffern. | |
|
Beispiel |
|
|
♦
|
Im Schullabor wird die Masse m eines Aluminiumstücks mit einer Präzisionswaage ausgemessen. Die Waage zeigt 41,952 g – auf Milligramm genau, d.h. ± 0,0005. Unterer und oberer Wert im Rahmen der Messgenauigkeit: 41,9515 g < m < 41,9525 g |
| ♦ | Das Volumen V wird via Eintauchen bestimmt auf 15,4 cm3 – die Messgenauigkeit beträgt ± 0,2 cm3. Unterer und oberer Wert im Rahmen der Messgenauigkeit: 15,2 cm3 < V < 15,6 cm3 |
| ♦ |
Mit den gemessenen Werten wird nun die Dichte ρ berechnet.
Unterer und oberer Wert der Dichte im Rahmen der Messgenauigkeit:
Eine vernünftige Angabe des Messresultates mit (Maximal-) Fehler ist dann
|
Drachenviereck
Drehung
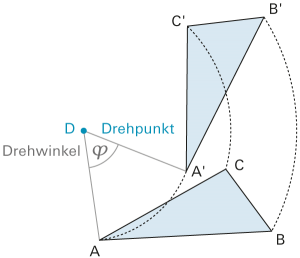 |
|
Die Drehung ist eine Kongruenzabbildung. |
|
Spezialfall: |
Dreieck
| 1 |
In einem Dreieck werden die Eckpunkte üblicherweise im Gegenuhrzeigersinn mit Grossbuchstaben in alphabetischer Reihenfolge beschriftet, zum Beispiel mit A, B, C. Die Seiten bezeichnet man dann meistens mit den entsprechenden Kleinbuchstaben a, b, c, wobei a der Ecke A gegenüberliegt, b der Ecke b und c der Ecke C. Der Winkel bei Punkt A heisst dann α («Alpha»), der Winkel bei B heisst β («Beta») und derjenige bei C heisst γ («Gamma»). |
||||||||||||||||
|
|
|||||||||||||||||
| 2 |
Dreiecke kann man nach Winkelgrössen oder Seitenlängen einteilen. Die längste Seite liegt immer dem grössten Winkel gegenüber. |
||||||||||||||||
|
|||||||||||||||||
|
|
|
||||||||||||||||
|
3 |
Der Flächeninhalt ist beim Dreieck halb so gross wie das Produkt aus einer Seitenlänge und der Länge der zugehörigen Höhe. | ||||||||||||||||
 |
|||||||||||||||||
Dualsystem
| siehe Binärsystem |
Durchschnittswert
|
siehe Mittelwerte |
Einheiten
|
Beim Messen von Grössen braucht man (Mass-) Einheiten als Vergleich. |
|
|
Beispiele: |
| Längen misst man z.B. in | m, dm, cm, mm, km |
| Flächen misst man z.B. in | m2, dm2, cm2, mm2, a, ha, km2 |
| Volumina misst man z.B. in | cm3, dm3, m3 – aber auch in ml oder l |
| Zeit misst man z.B. in | s, min, h |
| Massen misst man z.B. in | kg, g, mg, t |
| Geschwindigkeiten in | km/h, m/s |
| Dichten in | g/cm3, kg/m3 – aber auch in kg/dm3 |
Einsetzungsverfahren
| Verfahren zur algebraischen Lösung eines linearen Gleichungssystemes. | |
| Gegeben seien zwei Gleichungen: |
|
| Schritt 1 G1 auf x lösen. |
|
|
Schritt 2 |
|
| Schritt 3 Ergebnis in Gleichung G1 einsetzen und die Gleichung auf x lösen. |
|
| siehe auch Additionsverfahren und Gleichsetzungsverfahren | |
Entwicklungsfaktor
|
Beträgt die «Wachstumsrate» r bei exponentiellem Wachstum zum Beispiel 2%, so ändert sich die betrachtete Grösse pro Zeitschritt offenbar um den konstanten Faktor 1,02. |
|
Die Zahl q = 1 + r heisst «Entwicklungsfaktor» oder «Wachstumsfaktor». Bei exponentieller Abnahme («Zerfall») ist r negativ und 0 < q < 1. |
erweitern
| Siehe Bruchoperationen |
euklidischer Algorithmus
|
Der euklidische Algorithmus beschreibt ein Verfahren, mit dem der |
| siehe Algorithmus |
eulerscher Polyedersatz
exponentieller Zerfall
| Nimmt eine Grösse in gleichen Zeitschritten um immer den gleichen Prozentsatz ab, spricht man von «exponentiellem Zerfall» oder «exponentieller Abnahme». |
|
Beispiel |
|
|
| Siehe auch radioaktiver Zerfall und Abschreibung |
exponentielles Wachstum
|
Nimmt eine Grösse B pro Zeitschritt (pro Sekunde, pro Stunde, pro Jahr, …) immer um den gleichen Prozentsatz zu, so spricht man von «exponentielles Wachstum». |
|
|
Die Wachstumsrate ist konstant: |
|
Im Koordinatensystem liegen die Punkte (t/B(t)) auf einer Kurve mit der Gleichung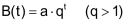 |
| Beispiele | |
|
♦ ♦ |
Kapitalentwicklung mit konstantem Zinssatz 2%: |
|
|
|
|
♦
|
Abnahme des Luftdruckes mit zunehmender Höhe: |
| siehe auch Abschreibung und Entwicklungsfaktor | |
Faktor
|
Siehe Multiplikation |
faktorisieren
| «faktorisieren» heisst «in Faktoren zerlegen». | |
| 1 | Beim Buchstabenrechnen oder bei Lösen von Gleichungen sind Ausklammern oder der Einsatz der Binomischen Formeln wichtige Techniken dazu. Umkehrung ist das Ausmultiplizieren, siehe Distributivgesetz. |
| 2 | Natürliche Zahlen, die nicht Primzahlen sind, lassen sich als Produkt darstellen. Die auftretenden Faktoren heissen Teiler der Zahl. |
| Wichtig ist die Zerlegung einer Zahl in lauter Primfaktoren, siehe Primfaktorzerlegung. | |
Fakultät
|
Drei verschiedene Objekte A, B und C kann man auf 3 ∙ 2 ∙ 1 Arten «permutieren»: Für die erste Position hat man drei Auswahlmöglichkeiten, für die zweite noch zwei und für die dritte Position bleibt bloss noch ein Objekt übrig. |
|||
|
Für n verschiedene Objekte gibt es folgende Anordnungsmöglichkeiten: |
|||
|
n ∙ (n - 1) ∙ (n - 2) ∙ 3 ∙ 2 ∙ 1 |
|||
|
Abkürzung für dieses Produkt ist der Ausdruck n! (gelesen «n Fakultät»). Seine Grösse wächst sehr schnell: |
|||
| Ein Beispiel: | |||
|
5! 10! 20! 70! |
= = = |
120 3'628'800 2,4 ∙ 1018 ergibt eine Zahl mit über 100 Stellen und überfordert auch einen gewöhnlichen Taschenrechner. |
|
| Siehe Permutation | |||
Fläche
|
Zweidimensionales Gebilde, dessen Grösse man durch Vergleich mit einer Einheitsfläche bestimmt. Oft wird die Grösse einer Fläche einfach «Fläche» genannt. |
|
Siehe auch Flächeninhalt |
Flächeneinheiten
|
Ein Quadrat mit der Seitenlänge 1 cm (das «Zentimeterquadrat») hat eine Fläche von 1 cm2, das «Meterquadrat» hat eine Fläche von 1 m2. |
|
|
Weil in einem Meterquadrat 100 · 100 Zentimeterquadrate Platz finden, |
|
| Weitere gebräuchliche Flächeneinheiten: | |
| 1 km2 | = 100 ha (Hektaren) |
| 1 ha | = 100 a (Aren) |
| 1 a | = 100 m2 |
| 1 m2 |
= 100 dm2 |
| 1 dm2 | = 100 cm2 |
Flächeninhalt
Formate
|
Schreibpapier oder Couverts sind in der Regel nur in bestimmten Grössen erhältlich. Diese «Formate» wurden durch das Deutsche Institut für Normierung (DIN) festgelegt und sind heute auch in der Schweiz gültig. |
|
Am vertrautesten ist uns das Format DIN-A. Bei allen (rechteckigen) Blättern dieses Types ist das Verhältnis der Seiten zueinander identisch: |
|
Aus einem DIN-A4-Blatt entstehen durch halbieren senkrecht zur längeren Seite zwei Blätter des Formats A5. |
 |
|
Die Fläche des Formates DIN-A0 beträgt 1m2. Somit betragen bei einem DIN-A4-Blatt die Seitenlängen etwa 210 mm bzw. 297 mm. |
Formvariable
| Variablen einer Gleichung, nach denen nicht aufgelöst wird, nennt man «Formvariablen» oder «Parameter». Die Lösung einer Gleichung mit Formvariablen hängt davon ab, welche Grössen man für die Formvariablen wählt. | |
| Beispiele | |
| ♦ ♦ |
Die quadratische Gleichung x2 + c = 0 hat nur für c < 0 jeweils zwei Lösungen. Die Funktionsgleichung y =a · (x – u)2 + v beschreibt alle quadratischen Parabeln. Erst durch die Wahl des Scheitelpunktes S (u / v) sowie des Formfaktors a wird eine ganz bestimmte Parabel definiert. |
Funktion
|
Oft gibt es zwischen zwei Grössen x und y einen Zusammenhang. Ist dieser so, dass jedem x genau ein y zugeordnet werden kann, so spricht man von einer «Funktion». |
|
Die Menge aller x-Werte nennt man «Definitionsbereich» oder «Originalbereich». |
|
x heisst meist «freie» oder «unabhängige» Variable. |
|
Beispielaufgabe |
|
Wertetabelle zur Aufgabe: |
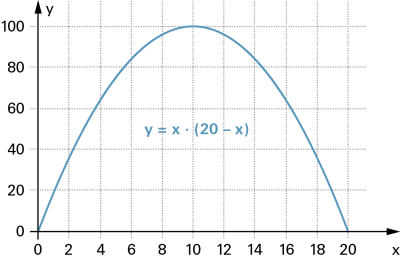
Die einzelnen Wertepaare lassen sich nach folgender «Funktionsgleichung» berechnen: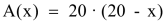 |
|
Der zugehörige Graph im Koordinatensystem zeigt die Entwicklung der Funktion (in unserem Beispiel die Entwicklung des Flächeninhaltes in Abhängigkeit von der Rechteckslänge). |
 |
|
siehe auch |
Funktionsterm
| Die Vorschrift, nach der zu einer freien Variablen der zugehörige Funktionswert berechnet wird, nennt man «Funktionsterm». |
|
Beispiel |
|
Überträg man die Wertepaare (x, y) als Punkte in ein Koordinatensystem, so liegen alle Punkte auf einer Parabel mit folgender Funktionsgleichung: |
ganze Zahlen
Geburtenüberschuss
| Als «Geburtenüberschuss» bezeichnet man die Differenz zwischen der Geburten- und Sterbezahl innerhalb eines Jahres. | |
| Unter der «Geburtenüberschussrate» versteht man den Geburtenüberschuss bezogen auf die Einwohnerzahl. | |
| Beispiel | |
| Geburten 80'000 Sterbefälle 70'000 Bevölkerung 8,2 Mio |
|
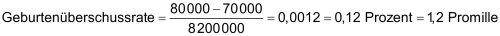 |
|
| Oft bezieht man die Geburtenüberschussrate auf 1'000 Einwohner und spricht dann von einer «Geburtenüberschussrate von 1,2». |
Geburtenüberschussrate
| siehe Geburtenüberschuss |
geometrisches Mittel
|
Das geometrische Mittel zweier positiver Zahlen ist definiert als Wurzel aus ihrem Produkt. |
|
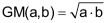 |
|
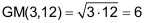 |
|
|
Geometrisch lässt sich das geometrische Mittel deuten als Seitenlänge jenes Quadrats, das den gleichen Flächeninhalt aufweist wie das Rechteck mit den Seitenlängen a und b. |
|
|
Konstruktiv findet man das geometrische Mittel mit dem Höhensatz. |
|
| siehe auch Mittelwerte | |
Geradengleichung
|
Jede mathematisch lineare Gleichung zwischen x und y wird im Koordinatensystem als Gerade dargestellt. Die «Geradengleichung» lässt sich – ausser im Fall einer Parallelen zur y-Achse – immer wie folgt schreiben: |
|
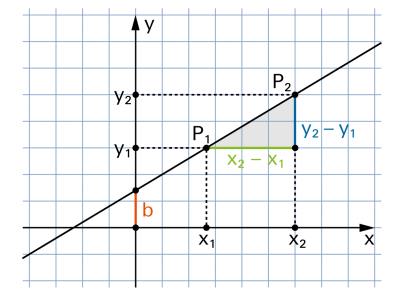 |
|
|
|
|
| a > 0 a < 0 a = 0 |
Die Gerade steigt mit wachsendem x. |
|
b ist der y-Achsenabschnitt. |
|
|
Jede lineare Gleichung der Form A ∙ x + B ∙ y + C = 0 beschreibt ebenfalls eine Gerade im Koordinatensystem. |
|
| Beispiele | |
| ♦ ♦ |
Die Gleichung y = 3 (beziehungsweise y – 3 = 0 ) beschreibt eine Parallele zur x-Achse im Abstand 3. Die Gleichung x + 2 = 0 beschreibt eine Parallele zur y-Achse links von dieser im Abstand 2. |
Geradenspiegelung
|
Siehe Achsenspiegelung |
Geschwindigkeit
|
Unter der (mittleren) Geschwindigkeit versteht man das Verhältnis zwischen dem zurückgelegtem Weg und der dazu benötigten Zeit: |
 |
| Man spricht hier auch von «Durchschnittsgeschwindigkeit». |
|
In vielen Fällen ändert sich das Tempo fortwährend. Die Geschwindigkeitsentwicklung lässt sich dann anhand von Diagrammen gut veranschaulichen: |
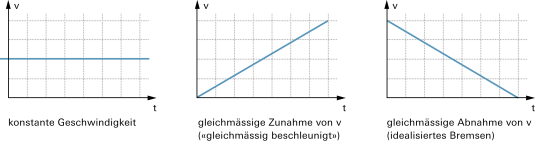 |
|
Im Weg-Zeit-Diagramm erscheint die (Momentan-)Geschwindigkeit als Steigung: |
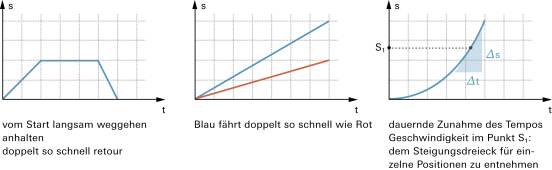 |
ggT
|
Die Abkürzung ggT steht für «grösster gemeinsamer Teiler» von zwei oder von mehreren Zahlen. |
|
Beispiel |
|
Für das Auffinden des ggT ist der euklidsche Algorithmus ein effizienter Weg, der auch leicht über eine Tabellenkalkulation zugänglich ist. |
gleichnamig
| Siehe Bruchoperationen |
gleichseitiges Dreieck
|
Beim gleichseitigen Dreieck sind alle Winkel gleich gross (60°). |
 |
| Da die Grösse eines gleichseitigen Dreiecks durch die Seitenlänge schon eindeutig bestimmt wird, lassen sich die Höhe h und der Flächeninhalt A aus der Seitenlänge allein berechnen: |
|
|
Gleichsetzungsverfahren
| Verfahren zur algebraischen Lösung eines linearen Gleichungssystemes. | |
| Gegeben seien zwei Gleichungen: | 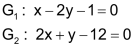 |
| Schritt 1 Beide Gleichungen auf x lösen. |
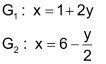 |
| Schritt 2 Beide Gleichungen gleichsetzen und auf y lösen. |
|
| Schritt 3 Das Ergebnis in Gleichung G1 einsetzen und die Gleichung auf x lösen. |
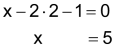 |
|
siehe auch Additionsverfahren und Einsetzungsverfahren |
|
Gleichung
|
Eine Gleichung besteht aus zwei Termen mit einer oder mehreren Variablen, die durch ein Gleichheitszeichen verbunden sind. |
||||||||
|
Eine «Gleichung lösen» heisst: |
||||||||
|
gleichwertig
| Terme, die beim Einsatz derselben Zahl für die Variable den gleichen Wert liefern, heissen gleichwertig oder äquivalent. |
| Siehe Äquivalenzumformung |
Grafik
|
Grafik ist Sammelbegriff für eine bildliche, oft geometrische Darstellung. |
|
Spezielle Beispiele: |
|
Siehe auch Graph |
Graph
|
Wird der Zusammenhang zweier Grössen in einem Koordinatensystem dargestellt, spricht man von einen «Graphen». |
|
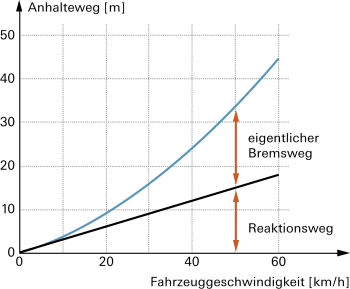
Beispiele: Füllgraphen, Weg-Zeitdiagramm, Anhalteweg eines Autos … |
 |
|
Wenn in einem Koordinatensystem der Zusammenhang zwischen zwei Grössen dargestellt ist, spricht man oft auch von «grafischer Darstellung», statt von «Graphen». |
|
 |
griechisches Alphabet
| In der Mathematik braucht man für Bezeichnungen oft auch griechische Buchstaben. Üblicherweise werden zum Beispiel Winkel mit griechischen Kleinbuchstaben bezeichnet. |
α |
Alpha |
ν |
Nü |
β |
Beta |
ξ |
Xi |
γ |
Gamma |
ο |
Omikron |
δ |
Delta |
π |
Pi |
ε |
Epsilon |
ρ |
Rho |
ζ |
Zeta |
σ |
Sigma |
η |
Eta |
τ |
Tau |
ϑ |
Theta |
υ |
Ypsilon |
ι |
Iota |
φ |
Phi |
κ |
Kappa |
χ |
Chi |
λ |
Lambda |
ψ |
Psi |
μ |
Mü |
ω |
Omega |
Grössen
|
Unter «Grössen» versteht man eine Verbindung von Zahl und Einheit. Oft spricht man präziser von «Masszahl» und «Masseinheit». |
|
|
Beispiele: |
|
|
17,5 m 4,9 l 18 cm3 |
|
|
Bei 10 m/s oder 2.50 Fr./kg oder 2,7 kg/dm3 spricht man von «zusammengesetzten Grössen». |
|
Grundmenge
|
Eine in der Statistik gebräuchliche Bezeichnung für einen untersuchten Bereich (Frauen, Männer, Jugendliche, Stimmberechtigte, Glühlampen, Laubbäume, …). |
|
Verlässliche Informationen über eine Grundmenge versucht man durch die Wahl einer geeigneten Stichprobe zu gewinnen. |
Grundoperationen
|
Als «Grundoperationen» bezeichnet man meist die Addition und die Subtraktion (beides Operationen erster Stufe) sowie die Multiplikation und die Division (Operationen zweiter Stufe). |
|
Das Wurzelziehen und Potenzieren gelten als Operationen dritter Stufe und zählen nicht zu den Grundoperationen. |
|
siehe Rechengesetze, Wurzel |
gültige Ziffern
| Messresultate ohne ausdrückliche Angabe des absoluten Fehlers sind immer so zu verstehen, dass die letzte Stelle gerundet ist: | |
|
♦ |
Die Angabe 17,4 m ist als «auf 3 gültige Ziffern genau» aufzufassen (± 0,05 m). |
| Bei Angabe von Messresultaten haben also auch Nullen am Schluss eine Bedeutung! | |
Halbwertszeit
|
Bei exponentiellem Zerfall gibt es einen Zeitschritt T, innerhalb dessen sich die betrachtete Grösse jeweils halbiert. Diese Zeit nennt man «Halbwertszeit». |
|
Wichtig ist dieser Begriff bei der Altersbestimmung nach der C14-Methode (für C14 beträgt |
Häufigkeit
|
Erscheint bei 100 Würfen mit einem Spielwürfel 14-mal die Zahl 6, so ist 14 die absolute Häufigkeit für die Augenzahl 6. |
|
|
Die relative Häufigkeit wird wie folgt angegeben (hier für die Augenzahl 6): |
|
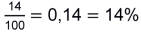 |
|
|
Sehr gebräuchlich ist bei relativen Häufigkeiten die Angabe in Prozent. |
|
|
Beispiel: |
|
|
In einem bestimmten Gebiet wurden auf eine Million Geburten 513 147 Knaben und |
|
|
Die relative Häufigkeit für Knabengeburten liegt hier ziemlich genau bei 51,3%. |
|
hekto-
Histogramm
|
Siehe Balkendiagramm |
Höhe
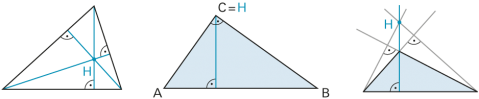
| 1 | Im Dreieck ist die Höhe die kürzeste Verbindungsstrecke von einer Ecke zur gegenüberliegenden Seite (oder der Verlängerung der Seite). |
 |
|
| Punkt H ist der Höhenschnittpunkt. Er liegt beim spitzwinkligen Dreieck innerhalb der Figur, beim stumpfwinkligen Dreieck ausserhalb. Beim rechtwinkligen Dreieck fällt er mit der Ecke beim rechten Winkel zusammen. | |
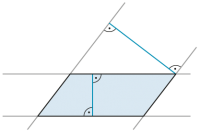
| 2 | Im Parallelogramm ist die Höhe der Abstand zweier paralleler Seiten. Sie entspricht der Streifenbreite. |
 |
|
|
Wie die Illustration zeigt, gibt es im Parallelogramm zwei verschiedene Höhen. |
|
| Siehe Dreieck, Linien im Dreieck |
Höhensatz
| «Im rechwinkligen Dreieck ist das Rechteck aus den Hypotenusenabschnitten gleich gross wie das Höhenquadrat.» |
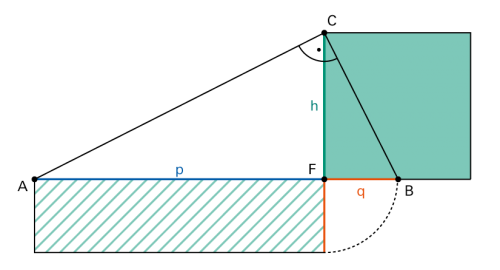 |
| Dass der Höhensatz stimmt, lässt sich zeigen über die Ähnlichkeit der Dreiecke AFC und FBC oder mit dem Satz von Pythagoras |
|
Konstruiert man ein rechtwinkliges Dreieck aus den Hypotenusenabschnitten p und q mit |
| siehe auch geometrisches Mittel |
Hohlmasse
| Siehe Volumeneinheiten |
Hyperbel
|
Die Graphen zur Funktion vom Typ |
|
Beispiele |
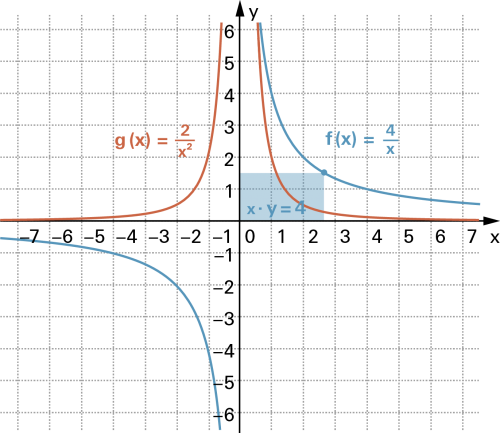 |
| Bei indirekter oder umgekehrt proportionaler Zuordnung ist der zugehörige Graph eine Hyperbel. Beispiel 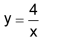 Das produktgleiche Zahlenpaar x · y = 4 erscheint als «eingebettetes Rechteck» mit immer gleicher Fläche, wenn die Ecke rechts oben auf der Hyperbel liegt. |
Hypotenuse
| Siehe rechtwinkliges Dreieck |
indirekt proportional
| Siehe unter umgekehrt proportional |
Inkreis
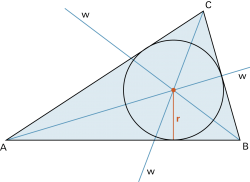
| Jedes Dreieck hat einen Inkreis. Sein Zentrum ist der Schnittpunkt der Winkelhalbierenden (w). |
 |
|
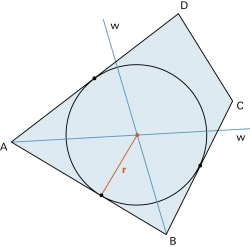
Vielecke mit mehr als drei Ecken haben im Allgemeinen keinen Inkreis. |
 |
|
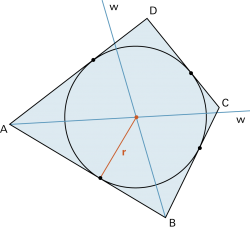
Ein Viereck mit Inkreis heisst Tangentenviereck. |
 |
Innenwinkel
|
Ein beliebiges n-Eck lässt sich in (n – 2) Dreiecke aufteilen. |
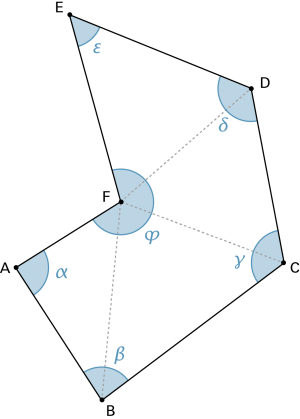 |
irrationale Zahlen
|
Zahlen, die sich nicht als Bruch in der Form In der Dezimalbruchdarstellung sind sie ... |
|
|
♦ |
weder abbrechend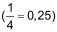 |
| ♦ | noch periodisch |
| ♦ | noch gemischt periodisch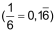 . . |
|
In der Darstellung unten liegen die irrationalen Zahlen im «weissen Bereich», also ausserhalb der rationalen, aber innerhalb der reellen Zahlen. Zusammen mit den rationalen Zahlen bilden die irrationalen Zahlen den Bereich der reellen Zahlen. |
|
 |
|
|
Siehe auch rationale Zahlen |
|
Isotope
|
Jedes Element hat – aufgrund seiner Protonenzahl im Kern – einen bestimmten Platz im Periodensystem. |
|
|
Weil sie im Periodensystem an der gleichen Stelle stehen, heissen sie «Isotope» (griechisch isotopos «gleiche Stelle»). |
|
|
Beispiele |
|
|
♦ |
C12 (natürliche Häufigkeit = 99%): |
Jugendquotient
|
Der «Jugendquotient» ist definiert als Verhältnis |
Karat
|
Die Reinheit von Gold wurde früher in «Karat» (kt) angegeben. |
|
Heute wird die Reinheit von Gold üblicherweise in Promille angegeben. Die Stempelung «750» in einem Schmuckstück bedeutet, dass die Legierung von 1000 Gewichtsanteilen 750 Anteile (d.h. drei Viertel) reines Gold enthält. |
kartesisch
| Siehe Koordinaten |
Kathete
| Siehe rechtwinkliges Dreieck |
Kathetensatz
| Im rechtwinkligen Dreieck hat das Kathetenquadrat die gleiche Fläche wie das Rechteck aus dem anliegenden Hypotenusenabschnitt und der Hypotenuse. |
|
Dieser Satz wird auch «Kathetensatz des Euklid» genannt. |
|
|
Kegel
|
Ein (gerader) Kreiskegel hat als Standfläche einen Kreis. |
|
|
Kreissektor |
|
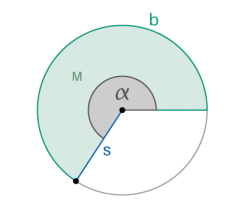 |
Bogenlänge b Mantelfläche M |
|
Grund und Aufriss des Kegels |
|
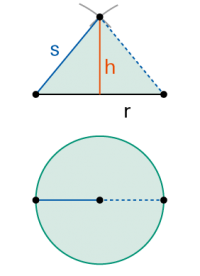 |
|
|
Schrägbild |
|
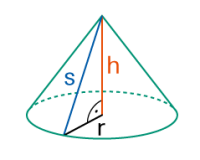 |
Volumen V Mantelfläche M |
Kegelstumpf
 |
Mantelfläche M Volumen V |
kilo-
Klammerregeln
| Siehe Rechengesetze |
Kombinatorik
|
Bei sehr vielen mathematischen Problemstellungen ist systematisches Zählen gefragt. Kombinatorik ist ein Teilgebiet der Mathematik und steht für «Kunst des Zählens». Oft hilft beim systematischen Zählen ein Baumdiagramm. |
|
Beispiel: |
|
Wie viele verschiedene Wege gibt es von A über B nach C, wenn man bei A unter drei und bei B unter zwei Wegen wählen kann? |
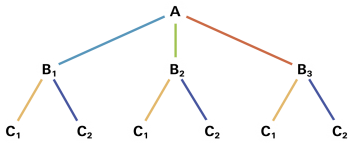 |
|
Aus dem Baumdiagramm ersieht man sofort, dass es 3 · 2 = 6 verschiedene Wege gibt. |
| Siehe auch Produktregel, Permutation und Lotto |
Komma
|
Das Komma trennt im Dezimalsystem die Stellenwerte zwischen Einern und Zehnteln. |
|
Grafisch erfolgt diese Trennung heute oft durch einen Punkt, den «Dezimalpunkt» (Taschenrechner, Computer). |
| Siehe auch Stellenwert |
Kommutativgesetz
| Siehe Rechengesetze |
konformer Zinssatz
| siehe Monatszins |
kongruent
|
Zwei Objekte sind «kongruent», wenn sie die gleiche Form und die gleiche Grösse haben. |
Kongruenzabbildung
|
Eine Kongruenzabbildung führt eine Figur in eine gleich grosse Figur von gleicher Form über. Dabei bleiben Winkel, Längen und Flächen der Figur unverändert. |
|
|
Die Achsenspiegelung, die Drehung, die Punktspiegelung und auch die Schiebung sind Kongruenzabbildungen. |
|
|
Achsenspiegelung: |
Drehung: |
Punktspiegelung: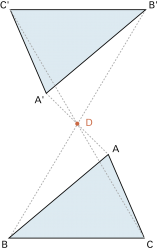 |
Schiebung: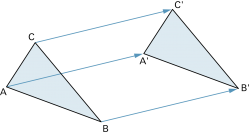 |
Kongruenzsätze
|
Dreiecke sind kongruent, wenn sie in drei (geeigneten) Stücken übereinstimmen. |
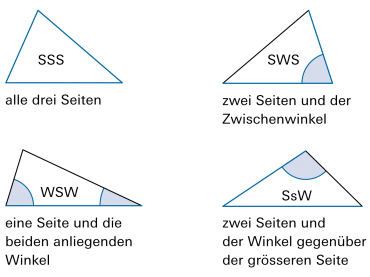 |
|
Das heisst auch: Wenn die drei Stücke vorgegeben werden, ist das Dreieck in Grösse und Form vollständig bestimmt. |
konvex
|
Ein Vieleck ohne einspringende Ecken wird «konvex» genannt. |
|
 konvexes Vieleck |
 nicht konvexes Vieleck |
|
Allgemein |
|
Koordinaten
 |
|
Legt man in die Ebene ein (kartesisches) Koordinatensystem, gehört zu jedem Punkt in eindeutiger Weise ein Zahlenpaar P(x/y). |
|
Normalerweise wählt man die x-Achse horizontal mit Richtungspfeil nach rechts (rot in der Abbildung), die y-Achse vertikal mit Richtungspfeil nach oben (blau in der Abbildung). |
|
Die erste Koordinate eines Punktes ist die x-Koordinate, die zweite Koordinate eines Punktes ist die y-Koordinate. |
|
Um die Lage eines Punktes im Raum eindeutig festzulegen, benutzt man drei paarweise aufeinander senkrecht stehende Achsen. Jeder Raumpunkt ist dann durch drei Koordinaten P(x/y/z) eindeutig festgelegt. |
Koordinatensystem
|
Ein Koordinatensystem ist ein Raster, das die Ebene (oder den Raum) so in genau lokalisierbare Teile zerlegt, dass die Lage eines Punktes, einer Geraden, einer Ebene oder eines Graphen durch eine Vorschrift (Zahlen, Gleichung) eindeutig auszumachen ist. |
| Siehe auch Koordinaten. |
Koordinatensystem, dreidimensional
|
Um die Lage eines Punktes im Raum eindeutig festzulegen, kann man ein «kartesisches Koordinatensystem» einsetzen (die drei Achsen x, y und z stehen paarweise senkrecht aufeinander). |
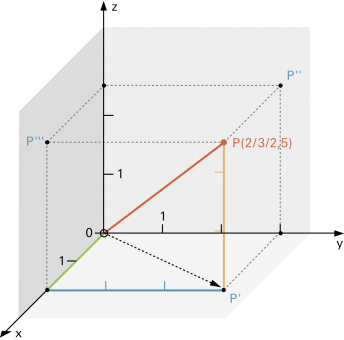 |
|
Den Punkt P (2/3/2,5) erreicht man vom Koordinatenursprung her, indem man sich 2 Schritte in x-Richtung, 3 Schritte in y-Richtung und dann 2,5 Schritte in z-Richtung bewegt. |
|
Das kartesische Koordinatensystem wird normalerweise als Rechtssystem bzw. rechthändiges System dargestellt: Daumen, Zeigfinger und Mittelfinger der rechten Hand zeigen in dieser Reihenfolge in x-, y- und in z-Richtung. |
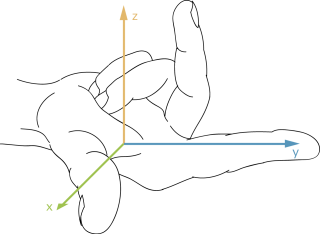 |
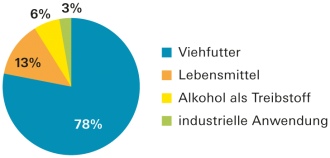
Kreisdiagramm
|
Im Kreisdiagramm (auch «Tortendiagramm» genannt) werden Anteile an einem Ganzen dargestellt. |
 |
Kreissektor
|
|
Sektorfläche As damit gilt für die Sektorfläche auch |
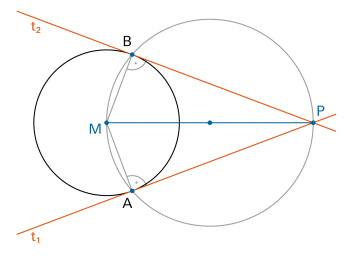
Kreistangente
|
Von einem Punkt P ausserhalb eines Kreises gibt es zwei Tangenten an den Kreis. |
 |
|
Siehe auch Kreisteile |
Kreisteile
|
Linien und Flächen am Kreis: |
 |
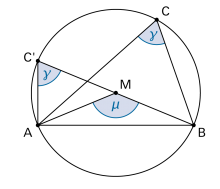
Kreiswinkelsätze
|
Für jeden Punkt C auf dem Bogen über AB gilt: Der zugehörige Peripheriewinkel (auch «Umfangswinkel» genannt) ist halb so gross wie der zugehörige Zentriwinkel: |
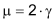 |
 |
|
Im Grenzfall |
|
Siehe Satz des Thales |
Kreiszahl π
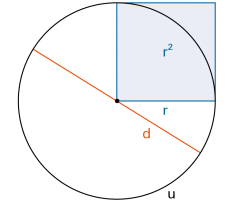
Die Kreiszahl π ist eine Verhältniszahl. Sie tritt entweder als Verhältnis von  oder auch von oder auch von 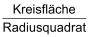 auf. auf. |
||
 |
||
|
π ist eine irrationale Zahl. Als Dezimalbruch dargestellt bricht π nicht ab und ist nicht periodisch. Gerundet auf 5 Stellen: π ≈ 3,14159 |
||
| Damit gilt für die Kreisfläche | AKreis = π ∙ r 2 | |
| und für den Kreisumfang | uKreis = 2π ∙ r = π ∙ d | |
|
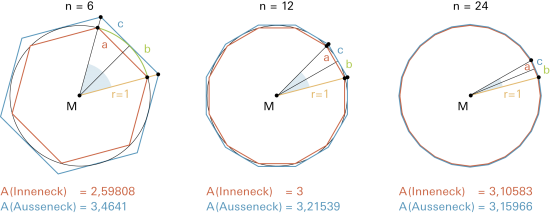
Ist ein Kreis Umkreis eines regulären n-Ecks und zugleich Inkreis eines regulären n-Ecks, kann seine Fläche durch Einschachteln mit wachsendem n immer genauer bestimmt werden. Man erhält so jeweils bessere Werte für π. |
||
 |
||
| Als Mittelwerte ergeben sich auf diesem Weg hier 3,03109, 3,10765 und 3,13275. | ||
Kugel
|
||||||
|
Das Prinzip von Cavalieri erlaubt die Herleitung der Fomel für das Kugelvolumen. Nach Segner sind die Querschnittsflächen einer Halbkugel und des Differenzkörpers aus Zylinder und Kegel mit Höhe h = r auf jeder Höhe gleich gross. |
||||||
|
kürzen
| Siehe Bruchoperationen |
Laplace-Formel
| Siehe Wahrscheinlichkeit |
Legierung
|
Eine Legierung ist eine Mischung aus verschiedenen Metallen. |
lineare Funktion
|
Funktionen, die im kartesischen Koordinatensystem dargestellt eine Gerade ergeben, bezeichnen wir als «linear». |
| siehe Geradengleichung |
lineare Gleichung
|
Eine Gleichung, bei der die Variablen nur in der ersten Potenz vorkommen, nennt man «linear». |
|
lineare Gleichung mit einer Unbekannten: |
|
lineare Gleichung mit zwei Unbekannten: |
lineares Gleichungssystem
|
Oft kann man eine Situation durch mehrere lineare Gleichungen beschreiben, die alle gleichzeitig erfüllt sein müssen. Zu einem solchen «Gleichungssystem» sind dann die gemeinsamen Lösungen gesucht. |
|
Liegen zwei lineare Gleichungen mit zwei Unbekannten vor, spricht man oft kurz von einem |
| Geometrisch entspricht einer linearen Gleichung mit zwei Unbekannten eine Gerade. Die Lösung eines 2x2-Systems kann damit über den Schnittpunkt der beiden entsprechenden Geraden grafisch bestimmt werden. |
 |
|
Zur algebraischen Lösung eines solchen Systems werden oft drei Verfahren angeboten: |
|
Das Gemeinsame an den drei Verfahren: |
lineares Wachstum
|
Nimmt eine Grösse B im Laufe der Zeit in gleichen Zeitschritten Δt immer gleich viel zu, so spricht man von «linearem Wachstum». |
|
| B(t+Δt) – B(t) = const. | |
|
Die Punkte (t/B(t)) liegen auf einer Geraden. |
|
Linien im Dreieck
Liniendiagramm
|
Das Liniendiagramm wird oft eingesetzt, um eine Entwicklung darzustellen: |
Lot
 |
|
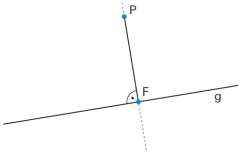
Die Zeichnung zeigt das Lot von Punkt P auf die Gerade g. |
|
Je nach Situation ist damit die Senkrechte (Gerade) oder bloss die Strecke von P nach F (dem «Lotfusspunkt») gemeint. |
magische Quadrate
|
In einem «magischen Quadrat» der Seitenlänge n sind n2 Zahlen so platziert, dass die Summe jeder Zeile, jeder Spalte und jeder der beiden Diagonalen gleich gross ist. |
|
Beispiel |
|
Üblich ist, dass in einem n x n – Quadrat die Zahlen von 1 bis n2 eingetragen sind. Es ist aber auch möglich, magische Quadrate zum Beispiel aus lauter geraden Zahlen oder lauter Primzahlen zu konstruieren. |
Mantelfläche
| Bei Zylinder und Prisma, Kegel und Pyramide (und ihren Stümpfen) unterscheidet man bei der Hülle zwischen Mantelfläche, Grund- und evtl. Deckfläche. | |
|
|
|
|
Beim Zylinder beträgt die Mantelfläche: |
|
|
M = 2π · r · h |
|
|
Beim geraden Prisma besteht die Mantelfläche aus lauter Rechtecken. Genau wie beim Zylinder beträgt ihre Grösse Höhe ∙ Umfang der Grundfläche. |
|
|
|
|
|
Die Oberfläche ist die Summe aller Flächeninhalte der begrenzenden Flächen, d.h. Mantelfläche + Grundfläche + wenn vorhanden Deckfläche. |
|
Massstab
|
«Massstab 1:100» heisst, dass 1 cm auf dem Plan 100 cm in der Wirklichkeit bedeuten. |
|
Beispiel: |
|
4 cm auf einer Karte mit Massstab 1:25'000 entsprechen 1 km Länge in der Wirklichkeit, denn: |
Median
|
Ordnet man Messwerte oder Ergebnisse einer Stichprobe der Grösse nach, teilt der «Median» die Stichprobe in zwei Teile mit gleichem Umfang. |
||||||
|
Beispiele |
||||||
|
||||||
| Der Median ist ein «Mittelwert», der in der Statistik häufig gebraucht wird. Er unterscheidet sich im Wert oft erheblich vom arithmetischen Mittel. | ||||||
| siehe auch geometrisches Mittel |
mikro-
milli-
Mittellinien
|
In einem Vieleck verbinden die Mittellinien zwei benachbarte Seitenmitten. |
|
Siehe auch Mittendreieck und Mittenviereck |
Mittelsenkrechte
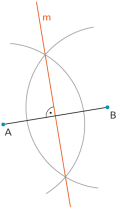 |
|
Alle Punkte, die von zwei gegebenen Punkten A und B gleich weit entfernt sind, liegen auf der Mittelsenkrechten zur Strecke von A nach B. |
| Siehe Linien im Dreieck |
Mittelwerte
| siehe arithmetisches Mittel, Median und auch geometrisches Mittel |
Mittendreieck
|
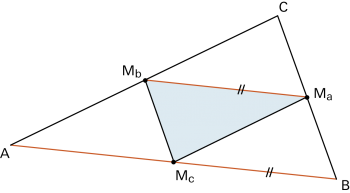
Verbindet man die Mitten Ma, Mb und Mc der Dreiecksseiten, so erhält man das Mittendreieck. |
|
 |
|
|
Merke: |
|
| • |
Jede Mittellinie ist parallel zur gegenüberliegenden Dreiecksseite und halb so lang wie diese. |
| • | Dreieck und Mittendreieck sind ähnlich zueinander, ihre Flächen verhalten sich wie 4 : 1. |
Mittenviereck
|
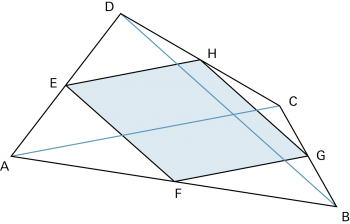
Im Viereck ist das Mittenviereck immer ein Parallelogramm. |
 |
|
Die Mittenverbindung |
|
Im Rechteck ist das Mittenviereck ein Rhombus und umgekehrt. Weiter ist die Fläche des Mittenvierecks halb so gross wie jene des Ausgangsvierecks. |
Monatszins
|
Bei Abzahlungsgeschäften wird das noch nicht zurückbezahlte Geld mit einem «Monatszins» belastet. |
|
Ein Monatszins von 1% – dies entspricht einem Wachstumsfaktor q = 1 + 1% = 1,01 – führt innert 12 Monaten zu einem Wachstumsfaktor 1,0112 = 1,1268 oder zu einem realen Jahres-zinssatz von 12,68%. |
|
Dies heisst umgekehrt: Bei einem Jahreszinssatz von 12% ist der Monats-Zinssatz (der «konforme Zinssatz») bloss näherungsweise 1%. Genauer müsste man mit 0,949 % rechnen. |
Multiplikation
|
Die Multiplikation ist eine Operation zweiter Ordnung. |
||
|
Eine Produkt ist … |
||
| a) | das Ergebnis einer Multiplikation: | |
| 3 · 4 = 12 | ||
| oder | ||
| b) | der (nicht ausgerechnete) Term, der durch das Malzeichen «zusammengehalten» wird: | |
| a · a2 5 · (3 + 8) c · (a + b) | ||
|
Beachte: |
||
|
Zwischen zwei Variablen oder zwischen einer Zahl und folgendem Buchstaben wird das Malzeichen oft weggelassen: |
||
| 3ab steht für 3 · a · b | ||
|
Die Glieder eines Produktes heissen «Faktoren». |
||
|
Siehe auch Rechengesetze und Bruchoperationen |
||
multiplizieren
|
Multiplizieren heisst «mal nehmen». |
| Siehe Multiplikation |
natürliche Zahlen
|
Natürliche Zahlen sind jene, mit denen man zählt. Für die unendliche Menge braucht man das Symbol |
|
Siehe auch rationale Zahlen |
negative Zahlen
|
Zahlen kleiner als 0 heissen negative Zahlen. |
||
|
Darstellung auf dem Zahlenstrahl: |
||
 |
||
|
Siehe auch rationale Zahlen |
Netz
|
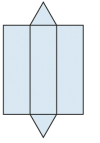
Netz eines (geraden) Dreiecks-Prismas (auch «Dreierprisma»): |
 |
|
Wenn man einen Körper längs einzelner Kanten so aufschneidet, dass sämtliche begrenzenden Flächen zusammenhängend auf einer Ebene ausgelegt werden können, so spricht man von einem «Netz» oder einer «Abwicklung» des Körpers. Ein Körper kann meist auf mehrere Arten aufgeschnitten werden. |
|
Siehe auch Prisma und Würfelnetze. |
Oberfläche
|
Unter der Oberfläche eines Körpers versteht man (meist) die Summe aller Flächeninhalte seiner Teilflächen. |
|
|
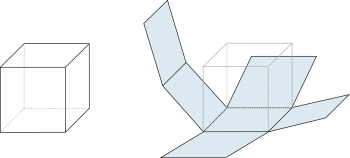
Beispiel: Würfel |
|
| S = 6 · a2 | |
 |
|
|
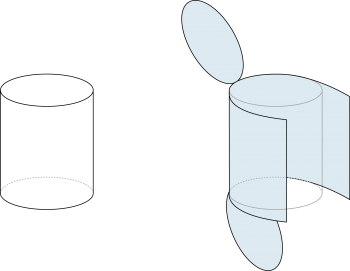
Beispiel 2: Gerader Kreiszylinder |
|
| S = 2 π r · h + 2 · π r2 | |
|
Man kann auch sagen: |
|
 |
|
Orientierung
|
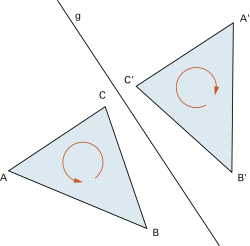
Mit «Orientierung» wird der Drehsinn einer Figur oder eines Winkels bezeichnet. |
 |
|
Das Dreieck ABC ist positiv orientiert (im Gegenuhrzeigersinn), das gespiegelte Dreieck ist negativ orientiert (im Uhrzeigersinn). |
  |
|
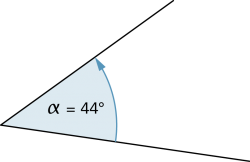
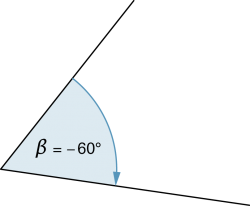
Wenn die Orientierung eines Winkels eine Rolle spielt, dann sind folgende Angaben üblich: |
Parabel
 |
|
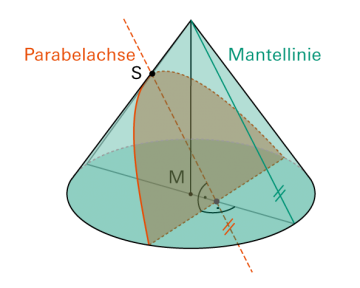
Schneidet man einen Kegel mit einer Ebene, die parallel zu einer Mantellinie verläuft, so ergibt sich als Schnittkurve eine «Parabel». |
|
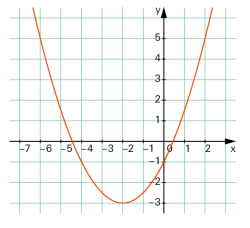
Stellt man diese Kurve im Koordinatensystem so dar, dass die y-Achse parallel zur Symmetrieachse der Parabel verläuft, kann man die Kurve mit einer quadratischen Funktionsgleichung beschreiben: |
| Umgekehrt ist der Graph einer solchen Funktion eine Parabel. |
 |
| siehe quadratische Funktion |
parallel
Parallelogramm
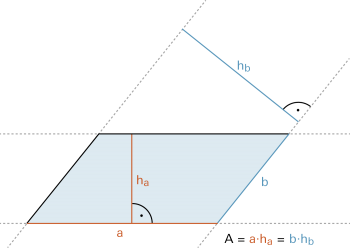
|
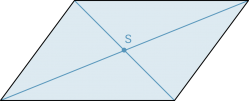
Das Parallelogramm (auch «Rhomboid») ist ein Viereck, bei dem die gegenüberliegenden Seiten parallel sind. |
 |
|
Beachte: |
| Jedes punktsymmetrische Viereck ist ein Parallelogramm, und umgekehrt ist jedes Parallelogramm ein punktsymmetrisches Viereck. |
 |
|
Fläche = Seitenlänge mal zugehörige Höhe (Höhe = Streifenbreite) |
Parameter
| siehe Formvariable |
parkettieren
|
Zum «Parkettieren» eignen sich (wenn man nur eine einzige Sorte Vielecke einsetzen will) das Quadrat, das Rechteck, das Parallelogramm und damit auch jedes Dreieck – aber auch ein allgemeines Viereck, ein reguläres Sechseck und diverse weitere Vielecke mit speziell abgestimmten Längen und Winkeln. |
|
Siehe auch reguläres Parkett, Penrose-Parkett |
Penrose-Parkett
|
Nichtperiodische Parkette mit einer kleinen Anzahl verschiedener Bausteine, mit denen sich zwar parkettieren lässt, sich aber kein regelmässig wiederholendes Muster einstellt. Der Mathematiker Roger Penrose (* 1931) hat als einer der Ersten solche Parkette gefunden.
|
Peripheriewinkel
| Siehe Kreiswinkelsätze |
Permutation
| «Permutation» ist ein Begriff aus der Kombinatorik. Als Permutation bezeichnet man allgemein eine Um- oder Anordnung von Elementen einer Menge. |
|
Beispiel |
| Oft spricht man auch von «Permutationen einer Menge» und meint damit einzig die Anzahl der möglichen Anordnung ihrer Elemente. |
| Beispiel Bei fünf Elementen a, b, c, d und e gibt es 120 (= 5 · 4 · 3 · 2 · 1) Möglichkeiten, bei den erwähnten drei Ziffern gibt es 6 (= 3 · 2 · 1) Möglichkeiten unterschiedlicher Anordnung. |
| siehe auch Fakultät |
platonische Körper
|
Ein «platonischer Körper» ist ein regelmässiges Polyeder: Alle Begrenzungsflächen sind zueinander kongruente regelmässige Vielecke, und an jedem «Knoten» treffen gleich viele Vielecke aufeinander. |
|||
 |
|||
| Es gibt nur fünf platonische Körper. Grund: Alle Winkel an einem Knoten müssen zusammen weniger als 360° gross sein, und es müssen dort mindestens drei Flächen aufeinander treffen. Das kann nur erfüllt werden durch |
|||
| ♦ ♦ ♦ |
3 regelmässige Fünfecke 3 Quadrate 3, 4 oder 5 gleichseitige Dreiecke |
→ → → |
Dodekaeder Würfel Tetraeder, Oktaeder und Ikosaeder |
|
Jeder platonische Körper besitzt eine In- und eine Umkugel mit gemeinsamem Zentrum. |
|||
platonisches Parkett
| Siehe reguläres Parkett |
Polyeder
|
Aus dem Griechischen («Vielflächer») stammende Bezeichnung für einen Körper, der durch (ebene) Vielecke begrenzt wird. |
|
 |
|
|
Der abgebildete Kuboktaeder zum Beispiel kann durch gleichmässiges Abschleifen der Ecken eines Würfels je bis in die Kantenmitten erzeugt werden. Er besteht aus 6 Quadraten und 8 gleichseitigen Dreiecken, hat 12 Ecken und 24 Kanten. |
|
|
Wichtige spezielle Formen |
|
| ♦
♦ |
reguläre Polyeder (siehe platonische Körper) |
Polygon
| Bezeichnung aus dem Griechischen für Vieleck. |
| siehe auch Innenwinkel |
Potenz
| Ein Produkt aus mehreren gleichen Faktoren kann man als Potenz schreiben. |
|
3 • 3 • 3 • 3 • 3 = 35 |
 |
|
Für grosse (und auch für sehr kleine positive Zahlen) werden Zehnerpotenzen eingesetzt: Basis der Potenz ist dann die Zahl 10. siehe auch Potenzgesetze |
Potenzgesetze
|
Für Potenzen mit natürlichen Zahlen als Exponenten gelten folgende Gesetze (a bezeichnet die Basis, n und k die Exponenten): |
||
| Gesetz 1 | 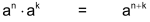 |
|
| Gesetz 2 | 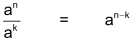 |
|
| Gesetz 3 | 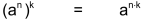 |
|
|
Bei Potenzen mit positiven Basen sind die Zahlen 0 und 1 sowie negative Zahlen als Exponenten sinnvoll. Dies lässt sich mit dem Gesetz 2 zeigen: |
||
 |
||
| Auch Brüche als Exponenten sind bei Potenzen mit positiven Basen sinnvoll. | ||
|
Laut Gesetz 3 gilt:
|
||
|
Aus der Definition der Wurzel folgt:
|
||
|
Weil das Ergebnis beider Gleichungen (im Beispiel = 10) identisch ist, gilt somit
(Vergleiche die Ausdrücke in den Klammern der beiden identischen Gleichungen.) |
||
|
Mit Taschenrechnern, welche eine «yx»-Taste haben, lassen sich so Wurzeln direkt berechnen. |
||
|
Beispiel
|
||
Primfaktorzerlegung
| Natürliche Zahlen, die nicht Primzahlen sind, lassen sich oft auf mehrere Arten in ein Produkt zerlegen. Die auftretenden Faktoren heissen Teiler. | |
| Wenn man als Faktoren nur Primzahlen wählt, heisst die Zerlegung «Primfaktorzerlegung». Die Primfaktorzerlegung ist eindeutig. | |
|
Beispiele: |
|
|
30 = 2 · 3 · 5 90 = 2 · 32 · 5 68'607 = 34 · 7 · 112 |
|
Primzahl
|
Bei den natürlichen Zahlen unterscheidet man die «Primzahlen» von den «zusammengesetzte Zahlen». |
||||||||||||||||||||||||||
|
Primzahlen lassen sich nur durch 1 und sich selbst teilen. Eine Primzahl hat demnach genau zwei (unechte) Teiler: die Zahl 1 und sich selbst. Die Zahl 1 ist nach diesen Kriterien keine Primzahl (sie hat nur einen Teiler). |
||||||||||||||||||||||||||
|
Es gibt unendlich viele Primzahlen. |
||||||||||||||||||||||||||
|
Zusammengesetzte Zahlen lassen sich in eindeutiger Weise in Primfaktoren zerlegen, aus denen sich alle Teiler der betreffenden Zahl gewinnen lassen. |
||||||||||||||||||||||||||
|
Beispiel: |
||||||||||||||||||||||||||
|
60 = 2 · 30 = 2 · 2 · 15 = 2 · 2 · 3 · 5 |
||||||||||||||||||||||||||
|
Folgende Zahlen sind echte Teiler von 60: 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 |
||||||||||||||||||||||||||
|
Primzahlen zwischen 1 und 100 |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
Primzahlen spielen beim Verschlüsseln von Dokumenten (Kreditkarten, Mailverkehr) eine zentrale Rolle. |
||||||||||||||||||||||||||
Primzahlzwillinge
|
Ausser bei den Zahlen 2 und 3 sind zwei Primzahlen immer mindestens zwei Schritte auf dem Zahlenstahl voneinander entfernt. Zwei Primzahlen, die sich um genau 2 unterscheiden, heissen «Primzahlzwillinge». |
|
|
Beispiele: |
|
|
(3;5), (5;7), (11;13), (17;19) aber auch (71;73) oder (1'019;1'021) |
|
|
Primzahlzwillinge werden «gegen oben» immer seltener. Stark zu vermuten ist, dass es trotzdem unendlich viele Primzahlzwillinge gibt. Erstaunlicherweise konnte dies aber bis heute nicht bewiesen werden. |
|
Prinzip von Cavalieri
|
Der italienische Mathematiker Bonaventura Cavalieri (etwa 1598-1647) hat das folgende Prinzip formuliert: |
|
Mit dem Prinzip von Cavalieri lassen sich zum Beispiel das Volumen eines schiefen Prismas, eines schiefen Zylinders oder auch das Kugelvolumen ermitteln. |
 |
Prisma
|
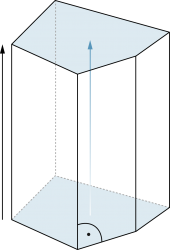
Verschiebt man ein Vieleck senkrecht zur Ausgangslage durch den Raum, so überstreicht es ein (gerades) Prisma. Grund- und Deckfläche sind kongruent, die Seitenflächen sind Rechtecke. |
 |
|
Quader und Würfel sind spezielle gerade Prismen. |
|
Erfolgt die Verschiebung des Vielecks nicht senkrecht («schräg») zur Ausgangslage, so spricht man von einem «schiefen Prisma». |
 |
Produkt
| Siehe Multiplikation |
Projektionen
|
Um räumliche Objekte auf einem Blatt Papier darzustellen, gibt es verschiedene Möglichkeiten: |
|
Zentralprojektion |
|
Parallelprojektion |
|
Fallen die Lichtstrahlen senkrecht auf die Bildebene, so spricht man von einer «senkrechten Projektion» oder «Normalprojektion». Fallen die Lichtstrahlen hingegen in einem andern Winkel auf redet man von einem Schrägbild. |
| Oft ist es vorteilhaft, von einem Objekt mehrere Normalbilder herzustellen, z.B. von oben, von vorne und von der Seite. Man spricht dann von «zugeordneter Normalprojektion». |
| siehe Risse |
Promille
|
Promille (‰) bedeutet «Tausendstel» (lateinisch PRO MILLE «von tausend»). |
|
Beispiel: |
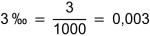 |
|
Promillegrenze: |
proportional
|
Zwei Grössen x und y heissen «proportional» zueinander, wenn das Verdoppeln (Halbieren, Dritteln, …) der einen Grösse das Verdoppeln (Halbieren, Dritteln, …) der anderen Grösse bewirkt. |
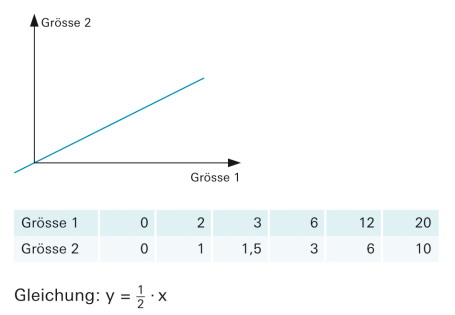
| Stellt man die proportionale Abhängigkeit zweier Grössen in einem Koordinatensystem dar, ergibt sich eine Gerade durch den Ursprung. |
|
In der Wertetabelle erkennt man Proportionalität daran, dass der Quotient aus zugeordneten Werten konstant ist, ausgenommen das Paar (0/0). |
 |
|
Die konstante Grösse k in der Gleichung y = k · x heisst «Proportionalitätsfaktor» oder «Proportionalitätskonstante». |
| Siehe auch umgekehrt proportional |
Prozent
|
Prozent (%) bedeutet «Hundertstel» (lateinisch PRO CENTUM «von hundert»). |
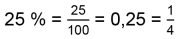 |
Punkt vor Strich
|
Diese Abmachung legt fest, dass beim Rechnen Mal- und Divisionszeichen («Punktoperationen», «Operationen zweiter Stufe») stärker binden als Plus- und Minuszeichen («Strichoperationen», «Operationen erster Stufe»). |
| Siehe Rechengesetze |
Punktoperation
|
Multiplikation und Division heissen «Punktoperationen», weil ihre Operationszeichen aus Punkten bestehen (Operationen zweiter Stufe). |
|
Siehe auch Punkt vor Strich |
Punktspiegelung
|
Die Punktspiegelung ist eine spezielle Kongruenzabbildung: Sie entspricht der Drehung einer Figur in der Ebene um einen Winkel von 180°. |
||
|
Konstruktiv ist sie – einfacher als durch einen Drehvorgang – wie folgt auszuführen: Das Bild P' eines Punktes P erhält man, indem auf einem Strahl von P durch den Drehpunkt D der Abstand auf die andere Seite abgetragen wird (der Drehpunkt D ist dann Mitte von ). ). |
||
|
Beispiel: |
Punktspiegelung eines Dreieckes ABC. | |
|
|
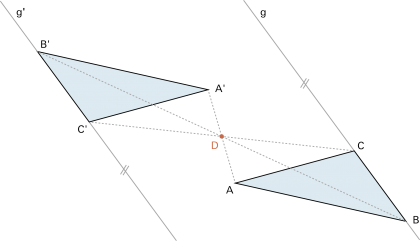 |
|
| Beachte: | Original und Bild einer Geraden sind jeweils parallel. | |
|
Punktsymmetrische Figuren |
||
| Gibt es bei einer Figur einen Drehpunkt D so, dass nach einer Drehung um 180° die Figur exakt gleich aussieht wie vorher, heisst sie «punktsymmetrisch». Den Drehpunkt D nennt man in diesem Fall auch «Symmetriezentrum». | ||
|
Propeller und viele Spielkarten sind punktsymmetrische Figuren. |
||
  |
||
|
Beachte: |
Jedes Parallelogramm ist ein punktsymmetrisches Viereck. | |
Punktsymmetrie
| Siehe Punktspiegelung |
Pyramide
| Pyramiden sind Körper mit einem n-Eck als Grundfläche und n Dreiecken mit gemeinsamer Spitze S als Mantelfläche. Höhe h ist der Abstand von S zur Grundfläche. | |
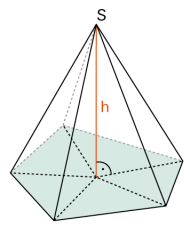 |
|
| Spezialfälle | |
| ♦ | einer «dreiseitigen Pyramide», d.h. man zählt die Standfläche nicht mit.) |
| ♦ | Regelmässige Pyramide: Die Grundfläche ist ein reguläres n-Eck, alle Kanten, die in S zusammenlaufen, sind gleich lang, damit liegt die Spitze S senkrecht über dem Mittelpunkt der Grundfläche. |
Pyramidenstumpf
 |
|
Mit G1 und G2 als Boden- und Deckelfläche ergibt sich das Volumen: |
Pythagoras-Satz
| Siehe Satz des Pythagoras |
Quader
Quadrat
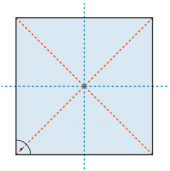 |
|
| Das Quadrat ist das regelmässigste Viereck. | |
|
• |
Es besitzt vier Symmetrieachsen. |
quadratische Ergänzung
| Zum Lösen einer quadratischen Gleichung der Form x2 + p · x + q = 0 bringt man diese in folgende, leicht lösbare Form: (x + r)2 = s |
|
 |
| Beispiel | |||
|
x2 + 10 · x – 20 |
= = = = = = = |
0 20 20 45 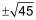 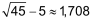 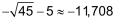 |
quadratische Funktion
|
Eine Funktion mit der Gleichung |
|
| Diese Funktion beschreibt eine (quadratische) Parabel. ♦ Für a > 0 ist die Parabel nach oben geöffnet, für a < 0 nach unten.♦ Ist |a| > 1, dann ist die Parabel «schlank». ♦ Für 0 < |a| < 1 ist die Parabel «ausladend». |
|
|
Man kann diese Vorschrift umformen zur Scheitelpunktsform: |
|
 |
|
|
In dieser Darstellung ist der Scheitelpunkt ist jeweils der tiefste oder der höchste Punkt der Parabel («Minimum» bzw. «Maximum»). |
quadratische Gleichung
|
Eine quadratische Gleichung hat allgemein die Form |
|
Durch Division der allgemeinen quadratischen Gleichung durch a erhält man die «Normalform»: |
| Grafisch ist das leicht einzusehen: |
|
Die Parabel mit der Gleichung |
|
Beim Lösen der Gleichung hilft die quadratische Ergänzung. |
|
Wenn der Ausdruck D = p2 – 4q > 0 ist, hat die Gleichung zwei Lösungen, |
| siehe auch quadratische Funktion |
quadratisches Wachstum
|
Eine Grösse y kann in Abhängigkeit von einer andern Grösse x nicht nur linear oder exponentiell, sondern auch zum Beispiel «quadratisch» (mit x2) oder mit der dritten Potenz (mit x3) wachsen. |
|
Beispiel |
Quadratwurzel
|
Die positive Lösung der Gleichung x2 = a (für a > 0) ist x = «Quadratwurzel aus a». Geschrieben wird die Quadratwurzel aus a als In der Schule wird statt «Quadratwurzel» oft einfach «Wurzel» gesagt. Statt «Quadratwurzel aus a» sagt man «Wurzel a». |
|
|
In den meisten Fälllen ist |
|
| Beispiel | |
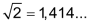 |
|
|
Siehe auch Wurzel, Potenzgesetze |
|
Quersumme
|
Die Summe der Ziffern einer Zahl heisst «Quersumme». |
|
Beispiel |
| Die Teilbarkeit einer Zahl durch 3 oder durch 9 lässt sich leicht über die Quersumme ermitteln. |
Quotient
|
Siehe Division, Rechengesetze und Bruchoperationen |
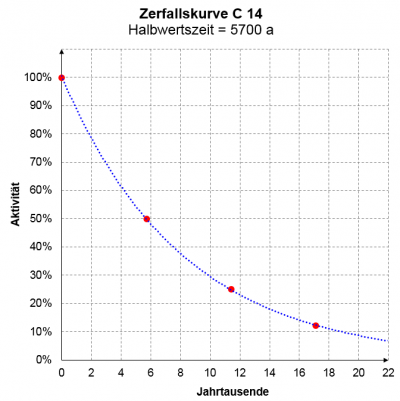
radioaktiver Zerfall
|
Viele Isotope eines Elements sind instabil: |
 |
rationale Zahlen
Alle Zahlen, die sich als Bruch in der Form 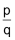 darstellen lassen, heissen rationale Zahlen (p und q sind ganzzahlig mit q ≠ 0). Abgekürzt wird diese Menge mit dem Symbol darstellen lassen, heissen rationale Zahlen (p und q sind ganzzahlig mit q ≠ 0). Abgekürzt wird diese Menge mit dem Symbol 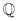 . Auch die ganzen Zahlen gehören zu dieser Menge. . Auch die ganzen Zahlen gehören zu dieser Menge. |
||
| Statt als Bruch kann eine rationale Zahl im Zehnersystem auch als abbrechender oder periodischer Dezimalbruch geschrieben werden: | ||
| • | ganz oder abbrechend: | 4 3,5 0,875 |
| • | periodisch: | 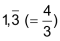 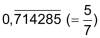 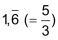 |
| Dezimalbrüche, die nach dem Komma und vor der Periode eine oder mehrere Ziffern aufweisen, werden oft «gemischt-periodisch» genannt: | ||
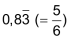 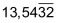 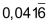 |
||
| Mit den rationalen Zahlen kann man uneingeschränkt addieren, subtrahieren und multiplizieren. Man kann auch uneingeschränkt dividieren, ausser durch 0. Das Ergebnis einer solchen Operation ist immer wieder eine rationale Zahl. | ||
 |
||
Nicht in den Bereich der rationalen Zahlen fallen Zahlen wie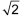 oder π, die sich in Dezimalbruchdarstellung weder als abbrechend noch als periodisch (oder gemischt periodisch) erweisen – und sich damit auch nicht als Bruch darstellen lassen. oder π, die sich in Dezimalbruchdarstellung weder als abbrechend noch als periodisch (oder gemischt periodisch) erweisen – und sich damit auch nicht als Bruch darstellen lassen. |
||
| Siehe auch irrationale Zahlen | ||
Raumdiagonale im Quader
|
Durch zweimaliges Anwenden des Satzes von Pythagoras ergibt sich die Länge der Quader-Raumdiagonalen (dR). |
 |
|
Die Raumdiagonale eines Würfels mit Kantenlänge a beträgt: |
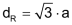 |
Rechengesetze
| Kommutativgesetz | a + b = b + a a · b = b · a |
|
|
|
|
Assoziativgesetz |
a + (b + c) = (a + b) + c a · (b · c) = (a · b) · c |
|
Distributivgesetz |
a · (b + c) = (a · b) + (a · c)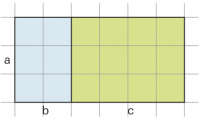 |
|
Zudem ist die Regel «Punkt vor Strich» zu beachten. |
|
|
|
|
|
Klammerregel 1 |
10 – (2 + 5) = 10 – 7 = 3 |
| Operationen in den Klammern rechnet man zuerst. | |
| Klammerregel 2 | 2 · (8 – (1 + 4)) = 2 · (8 – 5) = 2 · 3 = 6 |
| Bei ineinander geschachtelten Klammern rechnet man von innen nach aussen. | |
| Regel 3 | 7 · 8 : 4 = 56 : 4 = 14 |
| Rechnungen mit mehreren Punktoperationen rechnet man von links nach rechts. Beachte aber: | |
| 7 · (8 : 4) = 7 · 2 = 14 | |
| Regel 4 | 13 – 2 · 4 = 13 – 8 = 5 |
| Punktoperationen binden stärker als Strichoperationen. Beachte: |
|
| (a + b) · c ≠ a + b · c («Punkt vor Strich») | |
| Siehe auch Bruchoperationen | |
Rechteck
 |
|
|
Das Rechteck ist ein Viereck mit lauter rechten Winkeln. |
|
|
Weitere Eigenschaften des Rechteckes: |
|
|
• |
Die Diagonalen sind gleich lang. |
rechtwinkliges Dreieck
|
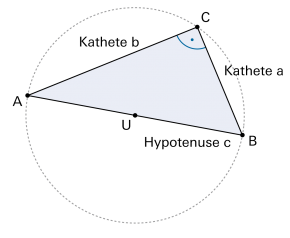
Das rechtwinklige Dreieck spielt in der Mathematik eine derart zentrale Rolle, dass seine Teile eigene Namen haben: |
 |
|
Für das rechtwinklige Dreieck gilt der Satz des Pythagoras: |
|
a2 + b2 = c2 |
reelle Zahlen
| Siehe irrationale Zahlen |
Regelmässiges n-Eck
|
Ein regelmässiges n-Eck ist eine ebene Figur mit n Ecken, bei der alle Seiten gleich lang und alle Innenwinkel gleich gross sind. |
|
|
Ein regelmässiges n-Eck hat sowohl einen Inkreis als auch einen Umkreis. |
|
|
Beispiele: |
|
|
gleichseitiges Dreieck, Quadrat, |
|
|
Der Innenwinkel im regelmässigen n-Eck beträgt: |
|
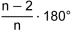 |
|
regulär
| Ausdruck für «regelmässig» |
| Siehe regelmässiges n-Eck |
reguläres Parkett
|
Ein Parkett heisst regulär, wenn ... |
|
|
1. |
alle Stücke regelmässige Vielecke (Polygone) sind, |
|
Wird nur eine einzige Sorte kongruenter regelmässiger Vielecke eingesetzt, heisst das Parkett platonisch. Offenbar gibt es bloss drei Möglichkeiten dazu: |
|
|
Wenn zwei oder mehr Sorten regulärer Vielecke eingesetzt werden, heisst das Parkett archimedisch. |
|
 |
|
| platonisch archimedisch weder-noch | |
| Siehe auch Vieleck, regelmässiges | |
relative Häufigkeit
| Siehe Häufigkeit |
relativer Fehler
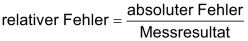 |
|
| Eine Messungenauigkeit von Δs = ±1 cm ist bei einer Länge von s = 20 cm natürlich viel einschneidender, als wenn die Länge s = 20 m beträgt. | |
|
♦ |
Relativer Fehler Δs = ±1 cm bei s = 20 cm: |
| ♦ | Relativer Fehler Δs = ±1 cm bei s = 20 m: 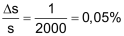 |
| Allgemein ist die Angabe des relativen Fehlers sinnvoller als die Angabe des absoluten Fehlers | |
Reste
|
Wenn man im Bereich der natürlichen Zahlen eine Zahl durch eine andere Zahl teilt, dann geht die Rechnung meistens «nicht auf», d.h. es bleibt ein ganzzahliger Rest. |
||
|
Beim Teilen einer natürlichen Zahl durch 7 zum Beispiel sind folgende Reste («7er-Reste») möglich: 1, 2, 3, 4, 5, 6 (Rechnung geht nicht auf) und 0 (Rechnung geht auf). |
||
|
Beispiel: |
||
|
55 hat den 7er-Rest 6 80 hat den 7er-Rest 3 |
||
|
a)
b) |
Multiplikation der beiden Zahlen: 55 · 80 = 4'400 →4'400 hat den 7er-Rest 4 Multiplikation der 7er-Reste beider Zahlen: 6 · 3 = 18 → 18 hat den 7er-Rest 4 |
|
| Siehe Teilbarkeit | ||
Rhomboid
| Siehe Parallelogramm |
Rhombus
|
|
|
|
Der Rhombus (die «Raute») ist ein Parallelogramm mit vier gleich langen Seiten. |
|
|
|
Für einen Rhombus gilt: |
Risse
|
Ein Körper wird auf drei Ebenen abgebildet (projiziert), die paarweise senkrecht aufeinander stehen. Diese Abbildungen heissen «Risse». |
|
Grundriss |
«von oben gesehen» |
| Für jeden Riss gilt: Die Projektionsstrahlen sind parallel und fallen senkrecht auf die Riss-Ebene. |
| Bemerkung In der Arbeitswelt wird oft die Seitenansicht eines Objekts mit Blick in die positive y-Richtung dargestellt. |
| siehe auch Projektionen und Schrägbild |
römische Zahlen
|
Im antiken Rom wurden die natürlichen Zahlen mit Buchstaben notiert. |
|
|
Für die Notation der römischen Zahlen gibt es einige Regeln, die aber nicht immer und überall strikt eingehalten wurden: |
|
|
♦ |
Zeichen mit hohem Wert stehen links, solche mit niedrigerem Wert rechts (wie in unserer Zahlnotation). |
|
Römische Zahlen |
Zehnersystem |
|
—————————————————— |
|
| MMCMLXI | 2961 |
| Weil bei den römischen Zahlen kein Positionssystem vorliegt, ist das Rechnen mit diesen Zahlen sehr schwierig. |
runden
|
Beim Rechnen entstehen oft Zahlen mit zu vielen Ziffern. Dann wird sinnvollerweise auf- oder abgerundet. |
| 27,6351 | auf Zehner gerundet | → | 30 |
| auf Einer gerundet | → | 28 | |
| auf Zehntel gerundet | → | 27,6 | |
| auf Hundertstel gerundet | → | 27,64 | |
| auf Tausendstel gerundet | → | 27,635 |
| Ist – von den wegfallenden Stellen – die am weitesten links liegende Ziffer … | |
| • | kleiner als 5, wird sie einfach abgeschnitten («abrunden»). |
| • | grösser oder gleich 5, wird die letzte bleibende Ziffer um 1 erhöht («aufrunden»). |
| Siehe auch Überschlag | |
Satz des Pythagoras
|
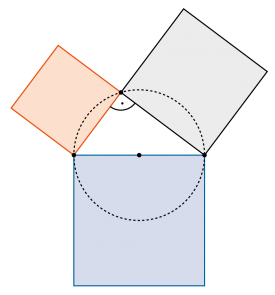
Im rechtwinkligen Dreieck ist die Summe der beiden Kathetenquadrate gleich gross wie die Fläche des Hypotenusenquadrats. |
 |
|
Wichtig ist auch die Umkehrung des Satzes: |
| siehe auch Höhensatz und Kathetensatz |
Satz des Thales
|
Der Winkel gegenüber einem Kreisdurchmesser, welches ein Dreieck mit einem Punkt auf den Kreis bildet, beträgt 90° (rechter Winkel). |
 |
|
Anders betrachtet: Der geometrische Ort aller Punkte, von denen aus eine vorgegebene Strecke |
|
Siehe Kreiswinkelsätze |
Säulendiagramm
| Siehe Balkendiagramm |
Scheitelpunkt
| siehe quadratische Funktion |
Scheitelpunktsform
| siehe quadratische Funktion |
Scheitelwinkel
| siehe Winkel an Geraden |
Schiebung
|
Wird eine Figur in eine bestimmte Richtung als Ganzes um eine bestimmte Strecke verschoben (Pfeil in der Abbildung), so spricht man von einer «Schiebung». |
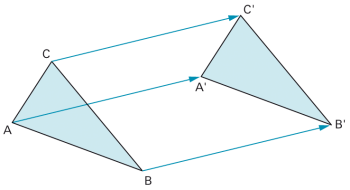 |
| Die Schiebung ist eine Kongruenzabbildung. |
Schrägbild
|
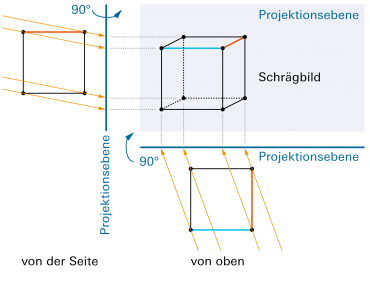
Wenn parallele Lichtstrahlen ein Objekt – zum Beispiel einen Würfel – beleuchten, so erzeugen sie auf einem Blatt ein ebenes (zweidimensionales) Bild. Man spricht von einem «Schrägbild», wenn die Strahlen schräg (d.h. in einem Winkel von |
|
 |
|
| Für Schrägbilder gilt: | |
| ♦ | Kanten, die parallel zur Bildebene stehen, haben im Bild die Originallänge. Winkel zwischen ihnen werden nicht verändert. |
| ♦ | Parallele Kanten sind auch im Schrägbild parallel. |
| ♦ | Mitte bleibt Mitte. |
| ♦ | Kanten senkrecht zur Bildebene werden alle um den gleichen Faktor verkürzt, z.B. auf zwei Drittel ihrer Originallänge. Meist wird das Bild am anschaulichsten, wenn eine Verkürzung auf etwa die Hälfte erfolgt. |
Schwerlinie
| Die Seitenhalbierende wird auch «Schwerlinie» genannt. |
| Siehe Linien im Dreieck |
Schwerpunkt
|
Im Dreieck ist dies der Schnittpunkt der drei Seitenhalbierenden (auch Schwerlinien genannt). Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 2 : 1. |
| Im Allgemeinen unterscheidet man bei ebenen Figuren zwischen einem Ecken-Schwerpunkt und einem Flächen-Schwerpunkt. Beim Dreieck fallen der Ecken-Schwerpunkt und der Flächen-Schwerpunkt zusammen. |
| Siehe auch Linien im Dreieck |
Segment
| Siehe Kreisteile |
Sehne
| Siehe Kreisteile |
Sehnenviereck
|
Ein Viereck mit Umkreis heisst Sehnenviereck. |
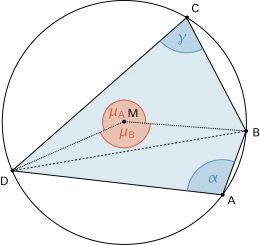 |
|
Im Sehnenviereck sind gegenüberliegende Winkel zusammen 180° gross, weil die zugehörigen Zentriwinkel sich auf 360° ergänzen. |
| Siehe auch Kreiswinkelsätze |
Seitenhalbierende im Dreieck
| Verbindung einer Dreiecksecke mit der Mitte der gegenüberliegenden Seite. Sie teilt das Dreieck in zwei flächengleiche Teildreiecke. |
| Siehe auch Linien im Dreieck |
Seitenmittendreieck
| Siehe Mittendreieck |
Sekante
| Siehe Kreisteile |
Sektor
| Siehe Kreisteile |
senkrecht
|
Wenn Geraden oder Strecken einen 90°-Winkel bilden, spricht man von «senkrecht stehen». |
 |
|
Gebräuchlich sind die beiden Darstellungen oben. |
|
Eine Gerade kann im Raum senkrecht auf einer Ebene stehen (man spricht auch vom «Lot auf einer Ebene»), und ebenso kann eine Ebene auf einer anderen Ebene senkrecht stehen: |
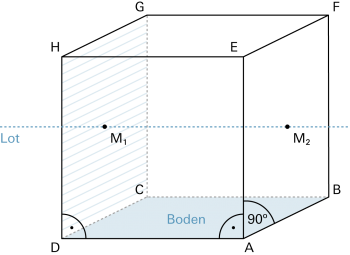 |
|
Die Strecke |
|
Die Ebene links durch die Seitenfläche DCGH steht senkrecht auf der Bodenebene ABCD. Die Gerade durch die Flächenmitten M1 und M2 steht senkrecht auf der Seitenfläche DCGH. |
SI-Einheiten
| Das Kürzel «SI» steht für «Système International d'Unités». | ||||
| Dahinter steckt eine internationale Vereinbarung zu den Masseinheiten. Grundgrössen werden festgelegt und physikalisch möglichst exakt definiert. | ||||
| Grundgrösse Länge Masse Zeit elektr. Stromstärke Temperatur |
Symbol l m t I T |
Grundeinheit Meter Kilogramm Sekunde Ampère Kelvin |
Abkürzung m kg s A K |
|
| Aus den Grundeinheiten bildet man die abgeleiteten Einheiten wie Joule (J) für die Energie, Watt (W) für die Leistung, Newton (N) für die Kraft, Hertz (Hz) für Frequenzen usw. | ||||
Stabdiagramm
|
Statt mit Rechtecken wie im Balkendiagramm werden Werte im Stabdiagramm durch vertikale Strecken dargestellt. |
Statistik
|
In der Statistik werden Daten gesammelt, dargestellt und ausgewertet (interpretiert). Statistik ist ein wesentliches Hilfsmittel in Naturwissenschaften, Soziologie, Ökonomie, Meteorologie, Medizin, Politik, Technik usw. und somit nicht mehr aus dem Alltag wegzudenken. |
Daten können in Tabellen oder als Grafiken dargestellt werden.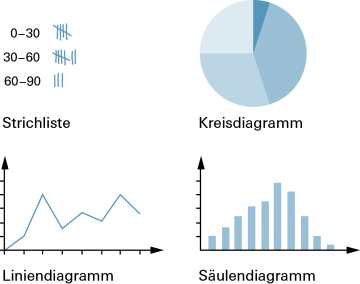 |
|
Von einer statistischen Untersuchung werden oft bloss wenige charakteristische Zahlen bekannt gegeben, zum Beispiel das arithmetische Mittel oder der Median. |
|
Hinweis Die einprägsame Darstellung mittels Bildern birgt in sich die Gefahr der Manipulation. Beim Interpretieren von Grafiken muss man deshalb besonders auf die ausgewählten Achsenabschnitte und auf eventuell verzerrte Achsenmassstäbe achten. |
Steigung
|
Bei einem Keil, einer Rampe, aber auch bei einer Geraden im Koordinatensystem ist die Steigung definiert als Verhältnis |
| Im Alltag spricht man auch von Gefälle statt von Steigung, wenn es abwärts geht. Bei der Geraden im Koordinatensystem hat die Steigung dann einen negativen Zahlenwert. |
 |
|
Zu einem Steigungswinkel von 45° gehört die Steigung 1 = 100% |
|
Siehe auch Geradengleichung |
Stellenwert
Stichprobe
|
Will man zur Wirksamkeit eines Medikamentes, zur Höhe der Wohnungsmieten in einer Stadt, zur Lebensdauer eines bestimmten Lampentyps, zum voraussichtlichen Ausgang einer Wahl, zu den Fernsehgewohnheiten von Jugendlichen in der Schweiz, … eine Auskunft haben, so zieht man aus dem zu untersuchenden Bereich eine «Stichprobe». |
|
An der Stichprobe führt man dann die notwendigen Untersuchungen durch und versucht aus den Resultaten eine verlässliche Aussage über die Grundmenge zu machen. |
Strahlensätze
|
Wird ein Dreieck AZB durch zentrische Streckung abgebildet, stehen auftretende Streckenlängen auf den Parallelen (in der Illustration blau) und den beiden Geraden |
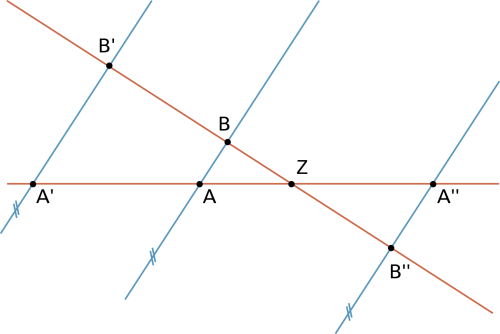 |
|
Beispiele
|
Streckenprofil
|
Ein Streckenprofil veranschaulicht grafisch einen Weg so, dass horizontal die Distanz zum Startpunkt und vertikal je die zugehörige Höhe über Meer (in überhöhtem Massstab) aufgetragen wird. |
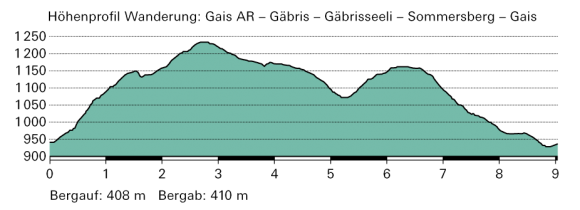 |
Streckenteilung
|
Wir zeigen die Teilung einer Strecke AB in n gleiche Teile am Beispiel von n = 5. |
|
Eine Hilfsgerade h wird durch den Anfangspunkt A gelegt. Dann werden auf dieser Geraden n gleich lange Strecken abgetragen. |
Streckfaktor
| siehe zentrische Streckung |
Streifenbreite
Strichoperation
|
Addition und Subtraktion heissen «Strichoperationen», weil ihre Operationszeichen durch Striche dargestellt werden (Operationen erster Stufe). |
| Siehe auch Punkt vor Strich |
Stufenwinkel
| siehe Winkel an Geraden |
subtrahieren
| Subtrahieren heisst «abzählen». |
| Siehe Subtraktion |
Subtraktion
| Die Subtraktion ist die Umkehroperation der Addition und somit eine Operation erster Ordnung. Das Operationszeichen ist das – («Minus»). | |||
| Eine Differenz ist … | |||
| a) | das Ergebnis einer Subtraktion: | ||
| 23 − 8 = 15 | |||
| oder | |||
| b) | der (nicht ausgerechnete) Term mit dem Minuszeichen als Hauptzeichen: | ||
|
23 − 8 3a − b (3a + b) − 2a |
|||
|
Siehe auch Rechengesetze |
|||
Symmetrieachse
|
siehe Achsenspiegelung |
Symmetriezentrum
|
siehe Punktspiegelung |
Tangente
|
Eine Tangente ist allgemein eine Gerade, die in einem Kurvenpunkt die gleiche Steigung hat wie die Kurve selbst. Leicht konstruierbar ist diese beim Kreis. |
| siehe Kreistangente |
Tangentenviereck
Teilbarkeit
|
Bei zahlreichen Problemen ist es wichtig, die Teiler einer natürlichen Zahl zu kennen. Für einige dieser Teiler gibt es einfache Kriterien bei der Suche: |
|
 |
|
| Für viele weitere Zahlen kann über die Teilbarkeit von einer Zahl z durch eine Kombination der oben angeführten Kriterien entschieden werden. | |
|
Beispielsweise ist z teilbar durch… |
|
| • | 6, wenn die Quersumme durch 3 teilbar und die letzte Ziffer gerade ist. |
| • | 15, wenn die Quersumme durch 3 teilbar und die letzte Ziffer eine 0 oder eine 5 ist. |
Teiler
|
Eine natürliche Zahl, die keine Primzahl ist, lässt sich oft auf mehrere Arten faktorisieren. |
|
|
Aus der Primfaktorzerlegung lassen sich alle Teiler gewinnen. |
|
| Beispiele: | |
| 42 = 2 • 3 • 7 |
(echte) Teiler von 42 sind |
| 60 = 22 • 3 • 5 |
(echte) Teiler von 60 sind |
Temperaturskalen
|
Die Temperatur beschreibt quantitativ den Wärmezustand eines Materials (Körper, Flüssigkeit, Luft, ...) |
|||
|
Gebräuchlich sind die |
|||
| • | Celsiusskala | Einheit °C, gleichmässige Unterteilung zwischen der Schmelz- und Siedetemperatur von Wasser (0 °C bzw. 100 °C) | |
| • | Kelvinskala |
Einheit K, gleiche Skalenschritte wie bei der Celsiusskala. Die Kelvinskala startet beim absoluten Nullpunkt –273 °C = 0 K, und damit sind 273 K = 0 °C und 373 K = 100 °C |
|
| • | Fahrenheitskala | Einheit °F, gleichmässige Teilung in 100 Schritten zwischen einer Kältemischung (0 °F) und der mittleren Körpertemperatur des Menschen (100 °F) | |
|
Umrechnung zwischen Celsius- und Fahrenheit-Skala: |
|||
| f = 1,8 ∙ c + 32 | c = (f – 32) : 1,8 | ||
|
(f und c stehen für die Anzahl Fahrenheit- bzw. Celsiusgrade) |
|||
Term
|
Mit «Term» bezeichnet man jede sinnvolle mathematische Zeichenreihe aus Zahlen, Variablen, Operationszeichen, Klammern, ... |
|
Werden in einem Term die Variablen durch Zahlen ersetzt und der Ausdruck ausgerechnet, so spricht man von «auswerten eines Terms». |
| Siehe gleichwertig und Äquivalenzumformung |
Thaleskreis
| Siehe Satz des Thales |
Thales-Satz
| Siehe Satz des Thales |
Trapez
| Ein Viereck mit einem Paar paralleler Seiten heisst Trapez. | ||||
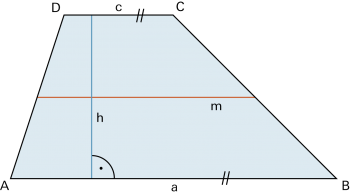 |
||||
|
Für die Mittenverbindung m gilt: |
||||
 |
||||
|
Damit kann die Fläche wie folgt berechnet werden: |
||||
|
A = m . h |
||||
| Siehe auch Achsentrapez | ||||
Überschlag
| Um das Resultat einer Rechnung im Kopf näherungsweise zu berechnen, vereinfacht man einzelne Bestandteile so, dass dies leichter möglich ist: | |
| Gefragt ist nicht ein «genaues Resultat», sondern eine sinnvolle, zweckmässige Genauigkeit. Das Ganze heisst dann «Überschlag» oder «Überschlagsrechnung». | |
|
Routinemässig wird mit gerundeten Zahlen überschlagen: |
|
|
• |
4'635 + 1'312 als 5'000 + 1'000 oder als 4'600 + 1'300 ... 3'124 • 243 ≈ 3'000 • 200 oder noch besser 3'000 • 250 |
| In vielen Situationen ist «stures» Runden (im Sinne von Auf- oder Abrunden) keine gute Strategie: | |
| • |
546 • 642 wird durch 500 • 600 zu schlecht geschätzt, besser macht man den einen Faktor kleiner und den anderen grösser, also 500 • 700 oder 600 • 600 |
| • |
8'765 : 26 ≈ 17'000 : 50 oder 34'000 : 100, also etwa 340; hier führt auch 9'000 : 30 auf einen guten Wert. |
| • | 237 • 16'398 ≈ 50 • 8'000 oder 1'000 • 4'000 (Verdoppeln und Halbieren als Strategie) |
| Durch Überschlag veränderte Zahlen müssen auch nicht unbedingt einfacher sein, es muss bloss «besser gehen» | |
| • | 100 : 15 ist etwa 105 : 15 |
| • |
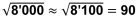 |
| Beim Rechnen mit Brüchen ist man gut beraten, wenn man einen Bruch durch einen einfacheren ersetzt: | |
| • |
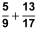 ist etwa ist etwa 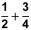 |
| oder man geht über zu Dezimalbrüchen und schätzt dann: | |
| • | 0,55 + 0,78 ≈ 0,6 + 0,7 bzw. ≈ 0,5 + 0,8 |
Umfang
|
Unter «Umfang» versteht man die Länge des Randes einer geschlossenen Figur. |
||
|
Beispiele: |
||
| Rechteck Kreis |
u = 2 · (a + b) u = 2π · r |
|
umgekehrt proportional
|
Ist das Produkt zweier einander zugeordneter Grössen x und y immer gleich gross, so spricht man von einer «umgekehrt proportionalen» Zuordnung (oft auch «indirekt proportional» genannt). |
|
Für umgekehrt proportionale Zuordnungen gilt: Das Verdoppeln der einen Grösse bewirkt das Halbieren der anderen Grösse. |
|
Die Darstellung im kartesischen Koordinatensystem ergibt eine Hyperbel. |
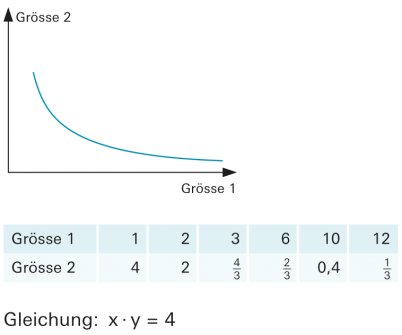 |
Umkreis
|
|
|
|
Jedes Dreieck hat einen Umkreis. Sein Zentrum ist der Schnittpunkt der Mittelsenkrechten. |
|
|
|
|
| Vielecke mit mehr als drei Ecken haben im Allgemeinen keinen Umkreis. | |
|
Vierecke, die einen Umkreis haben, heissen Sehnenvierecke. |
|
| Siehe Linien im Dreieck | |
Ungleichung
| Eine «Ungleichung» besteht aus zwei Termen mit einer oder mehreren Variablen, die durch ein Ungleichheitszeichen verbunden sind. | |
|
< |
«kleiner als» |
unlösbar
|
Wird eine Gleichung oder Ungleichung (mit einer Unbekannten) durch keine der zugelassenen Zahlen erfüllt, so spricht man von einer «unlösbaren Gleichung». |
|
Beispiel |
Ursprung
|
Mit «Ursprung» wird der Schnittpunkt der Achsen im Koordinatensystem bezeichnet. |
|
Die Koordinaten des Ursprungs sind somit in der Ebene (0/0) und im Raum (0/0/0). |
Variable
Verdoppelungszeit
|
Als «Verdoppelungszeit» bezeichnet man bei exponentiellem Wachstum jenen Zeitraum, innerhalb dessen eine Grösse auf das Doppelte anwächst. |
|
Für einen Wachstumssatz r mit 0 < r < 7% gibt es eine einfache Faustregel: |
Vieleck, regelmässiges
Vielfache
| Multipliziert man irgendeine Zahl a mit 1, 2, 3, 4, …, so entstehen Vielfache dieser Zahl a. |
| Zwei Zahlen können ein gemeinsames Vielfaches haben: |
| 36 ist Vielfaches sowohl von 6 als auch von 9 |
| Manchmal braucht man von zwei oder mehr Zahlen das kleinste gemeinsame Vielfache, abgekürzt kgV: |
| kgV (6, 9) = 18 kgV (3, 8) = 24 kgV (8, 12) = 24 kgV (4, 9, 12) = 36 |
|
Beachte auch Spezialfälle wie kgV (6, 12) = 12 |
Vierecke
| Die Einteilung («Systematik») von Vierecken ist nach verschiedenen Gesichtspunkten möglich. Eine Variante – ausgehend vom Quadrat als speziellstem Fall – stellen wir hier dar. |
|
|
|||||
 |
|||||
 |
|||||
 |
 |
||||
 |
 |
 |
 |
||
 |
 |
||||
|
|
Lesehilfen: Der Pfeil bedeutet «ist auch ein» Blaue Linie = Diagonale als Symmetrieachse Gestrichelte schwarze Linie = Verbindung gegenüberliegender Seitenmitten als Symmetrieachse Roter Punkt = Viereck ist punktsymmetrisch (der Punkt bezeichnet das Symmetriezentrum) |
|
|
Beispiele: Das Parallelogramm ist auch ein Trapez, da beide ein Paar parallele Seiten haben. Das Rechteck ist auch ein Achsentrapez («gleichschenkliges Trapez»), weil bei beiden eine Seitenmitten-Verbindung Symmetrieachse ist. Das Quadrat ist auch ein Parallelogramm, da beide punktsymmetrisch sind. |
Volumen
| Als Volumen (V) bezeichnet man den Rauminhalt oder das Fassungsvermögen eines Körpers. |
| Das Volumen ergibt sich durch Vergleichen mit Einheitswürfeln. Für bestimmte Körper gibt es Formeln, mit denen ihr Volumen berechnet werden kann. |
|
Siehe auch Volumeneinheiten |
Volumeneinheiten
| Ein Würfel mit Kantenlänge 1 cm – der Zentimeterwürfel – hat ein Volumen von 1 cm3. | |
| Ein Meterwürfel hat ein Volumen von 1 m3. In diesen Meterwürfel hinein passen 10 · 10 · 10 Würfel mit einem Dezimeter Kantenlänge, und in jeden dieser Dezimeterwürfel passen wiederum 10 · 10 · 10 Zentimeterwürfel. |
|
| 1 m3 = 1'000 dm3 = 106 cm3 | |
| Beachte: | |
| 1 km3 = 1'000 ⋅ 1'000 ⋅ 1'000 m3 = 109 m3 | |
| Bei Flüssigkeiten und Gasen wird das Volumen oft mit Hohlmassen angegeben. Gebräuchlichstes Mass ist der Liter (1 l). | |
| 1 l = 10 dl = 100 cl = 1'000 ml | |
| So hängen Volumeneinheiten und Hohlmasse zusammen: | |
1 dm3 = 1 l 1 l = 1'000 cm3 1 cm3 = 1 ml (1 mm3 = 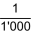 ml) ml) |
Vorsilben
Wachstumsfaktor
Wahrscheinlichkeit
|
Wahrscheinlichkeiten sind Prognosen für die relative Häufigkeit, mit der ein bestimmtes Ereignis bei einem Zufallsexperiment eintritt. |
|||
|
Als Platzhalter für Wahrscheinlichkeitswerte wird meist der Buchstabe p («probability») gewählt. Für p gilt immer 0 ≤ p ≤ 1, d.h. der Wert für eine Wahrscheinlichkeit ist nie kleiner als 0 und nie grösser als 1. |
|||
|
• • • |
Tritt ein Ereignis mit Sicherheit ein, so ist p = 1. Ein unmögliches Ereignis hat die Wahrscheinlichkeit p = 0. In allen anderen Ereignissen ist p grösser als 0 und kleiner als 1. |
||
|
Aufgrund von wiederholten Experimenten oder auch von Symmetrieüberlegungen sind Voraussagen über die Grösse von p möglich. |
|||
|
Besonders einfach ist die Berechnung der Wahrscheinlichkeit dann, wenn alle Möglichkeiten gleich wahrscheinlich sind. Dann rechnet sich die Wahrscheinlichkeit nach folgender Formel: |
|||
 |
|||
|
Diese Formel wird «Laplace-Formel» genannt. |
|||
|
Beispiel 1 |
|||
|
Bei einem Würfel treten im Mittel alle Augenzahlen mit gleicher relativer Häufigkeit auf, damit ist die Wahrscheinlichkeit… |
|||
|
• |
eine 6 zu werfen |
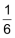 |
|
| • | eine gerade Augenzahl zu werfen | 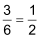 |
|
|
Beispiel 2 |
|||
|
Wirft man eine Münze zweimal hintereinander, so sind die möglichen Ergebnisse Dabei ist die Wahrscheinlichkeit für … |
|||
|
• |
zweimal Kopf |
|
|
| • | einmal Kopf und einmal Zahl | 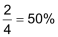 |
|
Wahrscheinlichkeitsbaum
|
In mehrstufigen Zufallsversuchen gibt oft ein Baumdiagramm eine gute Übersicht. Darin werden die Ausfälle und die zugehörigen Wahrscheinlichkeiten eingetragen. |
|
Beispiel |
|
Doppelwurf mit einem fairen Würfel: |
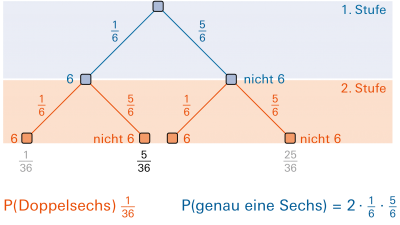 |
Wanderungsgewinn
|
Als «Wanderungsgewinn» bezeichnet man die Differenz zwischen der Anzahl Personen, die innerhalb eines Jahres in ein Land einwandern und der Anzahl Personen, die das Land verlassen. |
Wechselkurs
|
Der Wechselkurs ist der Preis einer Währung ausgedrückt in einer anderen Währung. |
|
|
Ankauf: Verkauf: |
Die Bank kauft meine Euros zu CHF 1.18 pro € Die Bank verkauft mir Euros zu CHF 1.22 pro € |
|
Die Ausdrücke «Ankauf» und «Verkauf» sind jeweils aus der Optik der Bank zu verstehen: |
|
Wechselsumme
|
Prüfkriterium für die Teilbarkeit einer Zahl durch 11. |
|||
|
Die Wechselsumme muss eine 11er-Zahl sein. |
|||
|
Wechselsumme bilden: |
|||
|
w = E ∙ 1 + Z∙ (–1) + H ∙ 1 + T ∙ (–1) + ∙∙∙ |
|||
|
(E ist die Einer-, Z die Zehnerziffer, H die Hunderterziffer etc.) |
|||
|
Beispiel: |
|||
|
z = 1'171'709 |
|||
|
→ Wechselsumme w = 9 ∙ 1 + 0 ∙ (–1) + 7 ∙ 1 + 1 ∙ (–1) + 7 ∙ 1 + 1 ∙ (–1) + 1 ∙ 1 = 22 |
|||
|
Beim Teilen von w durch 11 bleibt Rest 0, also ist auch z teilbar durch 11. |
|||
Wechselwinkel
| siehe Winkel an Geraden |
Wertetabelle
|
Zusammenhänge zwischen Grössen können in einer Wertetabelle festgehalten werden. Beispiel: |
| Menge [g] | 100 | 200 | 300 | 400 | 500 | 600 |
| Preis [CHF] | 3.00 | 6.00 | 9.00 | 15.00 | 22.50 | 30.00 |
| Die Wertepaare (Menge/Preis) lassen sich dann im Koordinatensystem anschaulich als Graph darstellen. |
Winkel an Geraden
|
Zwei sich schneidende Geraden bilden vier Winkel. |
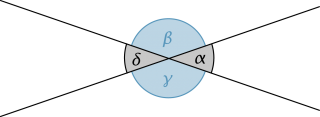 |
|
Zwei einander gegenüberliegende Winkel heissen «Scheitelwinkel». |
|
Zwei benachbarte Winkel heissen «Nebenwinkel». |
| «Stufenwinkel» an geschnittenen Parallelen sind gleich gross: α = β. «Wechselwinkel» an geschnittenen Parallelen sind gleich gross: δ = γ. 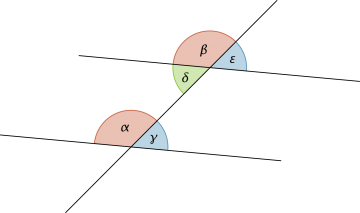 |
| siehe auch Winkelbezeichnungen |
Winkelbezeichnungen
|
|
Winkelhalbierende
Winkelhalbierende im Dreieck
| Die drei Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt – dem Inkreismittelpunkt. |
| Siehe Linien im Dreieck |
Winkelsumme
wissenschaftliche Schreibweise
|
In der Wissenschaft werden sehr gross oder sehr kleine Zahlen in folgender Form angegeben: |
|||
|
|
|||
|
Beispiele |
|||
|
für |
3'500'000'000 |
schreibt man |
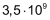 |
| für | 6'000'000'000'000'000'000 | schreibt man | 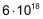 |
| für | 0,000'000'204 | schreibt man | 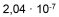 |
|
Die wissenschaftliche Schreibweise ist bei betragsmässig sehr grossen und sehr kleinen Zahlen sehr übersichtlich. Bei der Angabe von Messresultaten wählt man mit Vorteil ebenfalls die wissenschaftliche Schreibweise. Die Anzahl der Ziffern im Faktor a gibt dann Auskunft über die Genauigkeit der Messung. |
|||
|
Siehe auch Zehnerpotenzen |
|||
Würfel
| Der Würfel ist ein platonischer Körper mit vielen speziellen Eigenschaften. | ||||||||
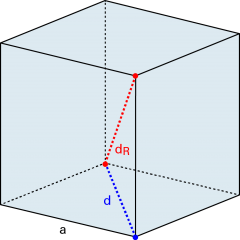 |
||||||||
|
||||||||
|
Ein Würfel besitzt je mehrere zwei-, drei- und vierzählige Symmetrieachsen. |
||||||||
 |
Würfelnetz
|
Mit «Würfelnetz» bezeichnet man sechs zusammenhängende Quadrate, die so angeordnet sind, dass daraus ein Würfel gefaltet werden kann. |
||
|
Zwei «Sechslinge», die zu einem Würfel gefaltet werden können:
|
||
|
Nicht alle Anordnungen von sechs Quadraten lassen sich zu einem Würfel falten. |
||
|
Ein «Sechsling», aus dem kein Würfel gefaltet werden kann: 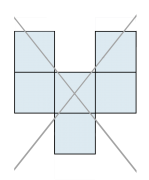 |
||
| Es gibt insgesamt 11 unterschiedliche Würfelnetze (Spiegelungen und Drehungen nicht mitgezählt). |
Wurzel [ zurück ]
|
Die positive Lösung der Gleichung xn = a (a > 0) wird als «n-te Wurzel aus a» bezeichnet und folgendermassen geschrieben: |
|
Beispiel |
|
Die positive Lösung der Gleichung |
|
Aus den Potenzgesetzen ergibt sich, dass für positive Zahlen die beiden Ausdrücke |
|
Damit gelten für das formale Rechnen mit Wurzeln die gleichen Regeln wie beim Nützlich ist oft (in beide Richtungen!) |
| siehe Potenzgesetze |
y-Achsenabschnitt
| siehe Geradengleichung |
Zahlen
|
Zahlen sind eine der bedeutendsten kulturhistorischen Erfindungen der Menschheit. Zuerst wurden Zahlen sicher zum Zählen gebraucht: 1, 2, 3, 4, … Diese Zahlen nennt man «Natürliche Zahlen». Kulturgeschichtlich kamen als Zweites die «Brüche» dazu, darauf die «Null», die für das Rechnen in einem Positionssystem unabdingbar ist. Bald wurde der Bereich der Brüche verlassen. Schon wenn man die Länge der Quadratdiagonalen sucht, verlässt man diesen Bereich: |
|
 |
Zahlengerade
|
Zahlen lassen sich der Grösse nach ordnen und geometrisch aufgereiht auf einer Geraden veranschaulichen: |
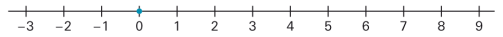 |
|
Zu jeder Zahl gehört ein bestimmter Ort auf der Zahlengeraden. |
|
Im Allgemeinen ist die Einteilung einer Zahlengeraden «aequidistant», d.h. die Zahl 2·a findet sich doppelt so weit von der Nullmarke entfernt wie die Zahl a. |
Zahlenmengen
| natürliche Zahlen | 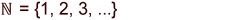 |
| ganze Zahlen | 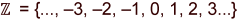 |
| negative ganze Zahlen | 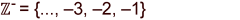 |
| rationale Zahlen |  |
| irrationale Zahlen |  |
|
|
|
Zehnerpotenz
|
Beispiele |
|||
| 1 Milliarde | = | 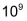 |
|
| 1 Billion | = |  |
|
| 1 Tausendstel | = | 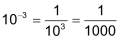 |
|
| 1 Millionstel | = | 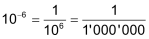 |
|
|
Beachte |
|||
|
|
|||
|
Siehe Potenzgesetze und wissenschaftliche Schreibweise |
|||
zentrische Streckung
| Die (zentrische) Streckung bildet einen Punkt P von einem Zentrum Z in einen Bildpunkt P' ab. | ||
| Abbildungsvorschriften | ||
| ♦ ♦ |
P' liegt auf der Geraden g(Z,P).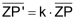 k heisst «Streckfaktor». Für k < 0 liegen Original und Bildpunkt auf verschiedenen Seiten des Streckzentrums Z. |
 |
| Eigenschaften | ||
| ♦ ♦ ♦ ♦ ♦ |
Bild und Original haben die gleiche Form (sind zueinander ähnlich). Bildstrecke und Originalstrecke sind zueinander parallel. Längen verhalten sich bei Bild und Original wie k : 1. Flächen verhalten sich bei Bild und Original wie k2 : 1. Volumina verhalten sich bei Bild und Original wie k3 : 1. |
 |
| Spezialfall Aus dem Dreieck ABC wird durch zentrische Streckung vom Schwerpunkt S aus mit k = –0,5 das Mittendreieck. |
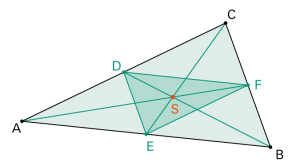 |
|
Zentriwinkel
| Siehe Kreiswinkelsätze |
Ziffer
|
Mit den zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9 stellen wir im Zehnersystem («Dezimalsystem») jede noch so grosse und auch jede beliebig kleine Zahl dar. |
|
3'490 = 3.103 + 4.102 + 9.101 3'492,5 = 3.103 + 4.102 + 9.101 + 2.100 + 5.10-1 |
|
Unsere Zahldarstellung ist eine Abkürzung für eine Summe von Zehnerpotenzen! |
|
Siehe auch Stellenwert-Tafel |
Zins
|
Der «Gläubiger» leiht dem «Schuldner» einen Geldbetrag B. Der Schuldner zahlt pro Jahr, in dem er beim Gläubiger in der Schuld steht, diesem einen «Zins» zu einem abgemachten Zinssatz von p%. |
|
Beispiel |
|
Für Laufzeiten von weniger als einem Jahr bezahlt man einer Bank den sogenannten «Marchzins». Er beträgt den Bruchteil (Laufzeit in Tagen : 360 Tage) vom Jahreszins. |
|
Beispiel |
| siehe auch Monatszins |
Zinseszins
|
Wird ein Kapital über mehrere Jahre angelegt und der Jahreszins immer wieder zum Kapital geschlagen, so spricht man von «Zinseszins». |
|
|
Bei einem Zinssatz von 3% beispielsweise gilt: und entsprechend |
|
|
Mit p% für den Zinssatz lautet die «Zinseszinsformel» |
Zufallsexperiment
| Man spricht von einem Zufallsexperiment, wenn der Ausgang einer Handlung vom Zufall gesteuert wird. Man kann im Einzelfall nicht voraussagen, welcher der möglichen Ausgänge (auch Ereignisse oder Ausfälle genannt) eintritt. |
zugelassene Zahlen
|
Es gibt Terme, die (zum Beispiel im Bereich der reellen Zahlen) nicht definiert sind oder keinen Sinn machen. |
|
|
Beispiele |
|
| ♦ |
|
| ♦ |
|
| ♦ | Die Gleichung x3 + y3 = z3 hat im Bereich der natürlichen Zahlen keine Lösung. Sie ist – wenn nur natürliche Zahlen zugelassen sind – unlösbar. |
|
Im Zusammenhang mit (Un-)Gleichungen oder Funktionen spricht man statt von «zugelassenen Zahlen» meist vom Definitionsbereich. |
|
Zweiersystem
| siehe Binärsystem |
Zylinder
|
Wird ein Kreis (Grundfläche) aus der Ebene heraus in eine konstante Richtung verschoben, so überstreicht er eine Zylinderfläche. |
|
 |
|
|
Die Zylinderachse entspricht der Verbindung vom Grundflächenmittelpunkt zum Deckflächenmittelpunkt. Eine Mantellinie m verläuft auf dem Mantel parallel zur Zylinderachse. |
|
|
Für das Volumen gilt: |
|
|
|
|
|
Oft versteht man unter «Zylinder» den geraden Kreiszylinder: Die Zylinderachse steht senkrecht auf den Kreisflächen. Andernfalls heisst der Zylinder schief. |
|
|
Mantelfläche beim geraden (Kreis-) Zylinder: |
|
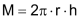 |
|
|
Siehe auch Oberfläche |
|


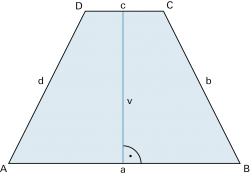
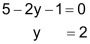
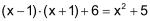
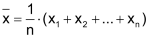
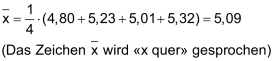
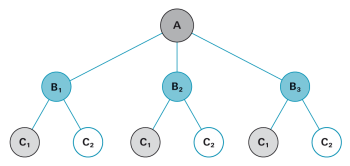

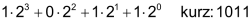
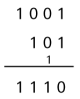

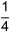
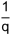

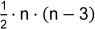 Diagonalen. Ein Sechseck hat somit neun, ein Fünfeck fünf Diagonalen.
Diagonalen. Ein Sechseck hat somit neun, ein Fünfeck fünf Diagonalen.
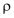 («Rho») bezeichnet:
(«Rho») bezeichnet: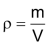
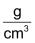

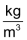
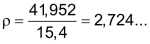
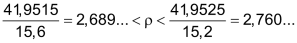
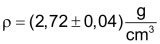
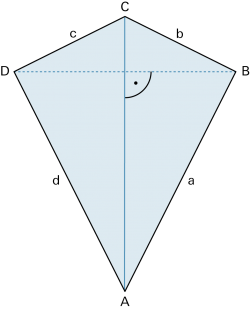
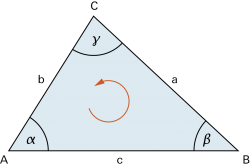

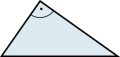

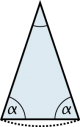
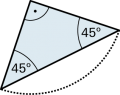
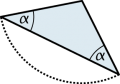
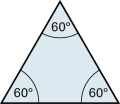
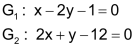
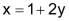
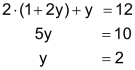
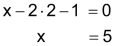
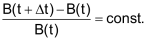
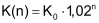
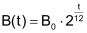
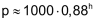

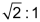

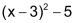
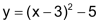


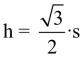
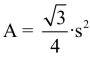
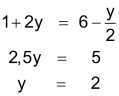
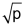
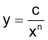
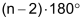
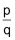

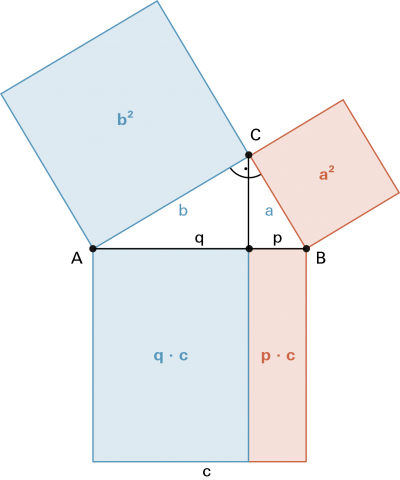
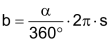
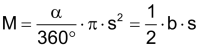
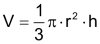
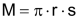
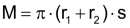
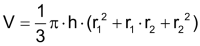
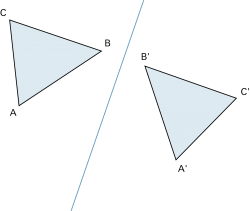
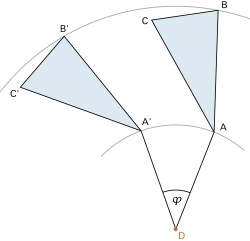
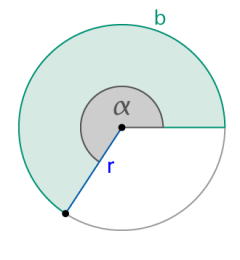
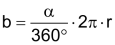
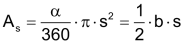
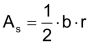

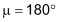 , in dem die Sehne AB zum Durchmesser wird, beträgt der
, in dem die Sehne AB zum Durchmesser wird, beträgt der 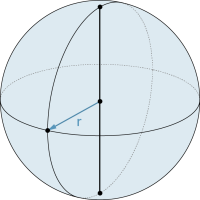
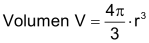

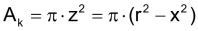
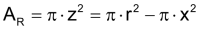
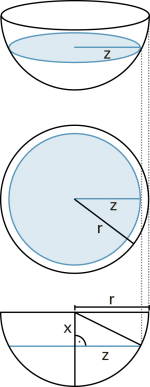
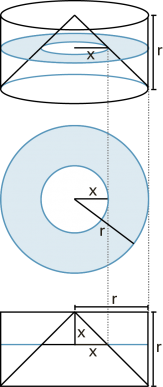
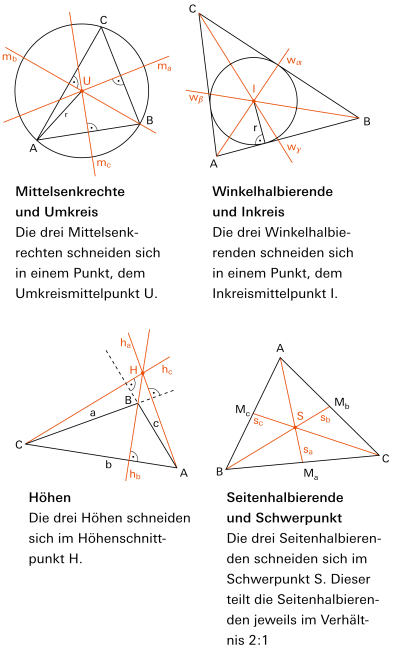
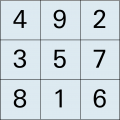

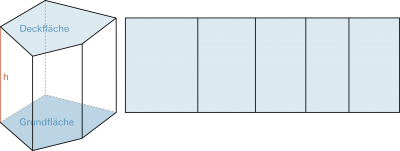
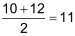
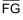 des Viereckes ist im Dreieck ABC auch Mittellinie (vgl. Illustration).
des Viereckes ist im Dreieck ABC auch Mittellinie (vgl. Illustration). oder auch die Schreibweise {1, 2, 3, 4, 5, ...}. 0 und die
oder auch die Schreibweise {1, 2, 3, 4, 5, ...}. 0 und die 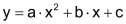
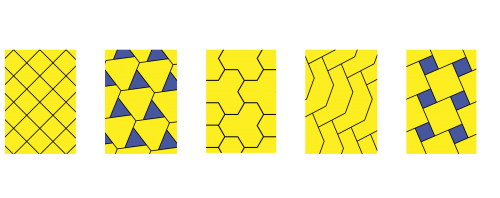

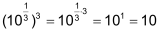
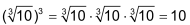
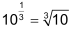
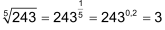
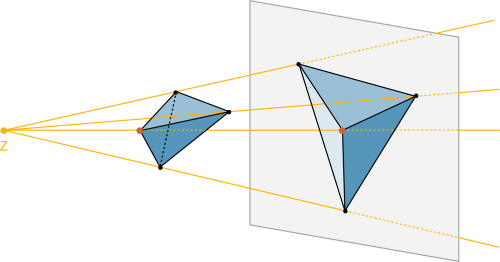
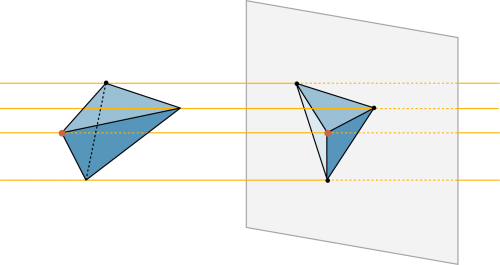
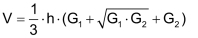
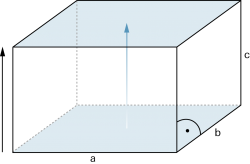
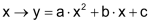
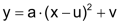
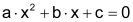
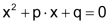
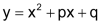
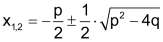
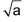 .
.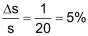
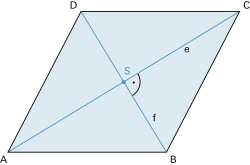
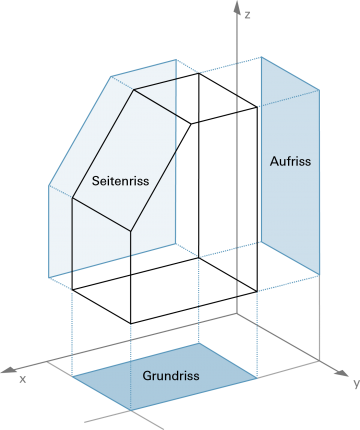
 unter einem rechten Winkel erscheint, ist der «Thaleskreis» über
unter einem rechten Winkel erscheint, ist der «Thaleskreis» über  steht senkrecht auf der Bodenebene ABCD. Die gleiche Strecke steht auch senkrecht auf der Strecke
steht senkrecht auf der Bodenebene ABCD. Die gleiche Strecke steht auch senkrecht auf der Strecke  und auf der Strecke
und auf der Strecke  .
.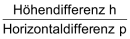 .
.
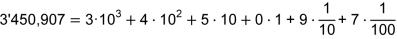
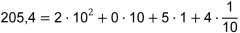
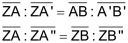
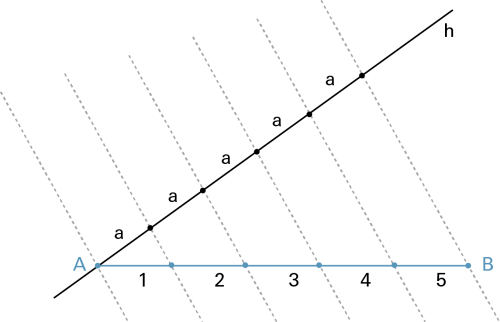
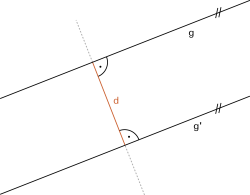
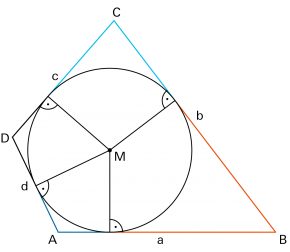
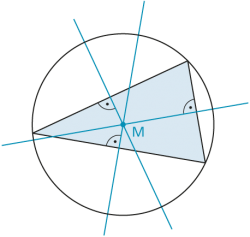
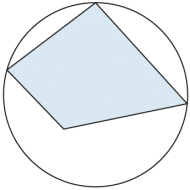
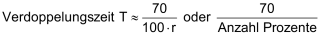
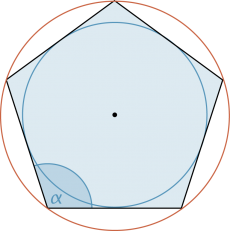
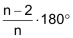



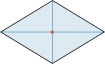
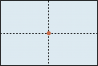
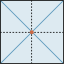

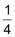
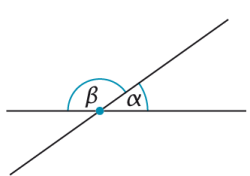



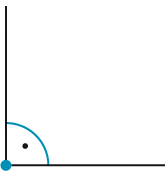

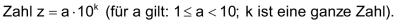
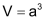
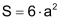
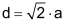
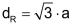
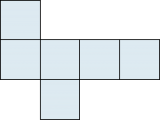
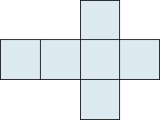
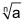

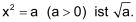

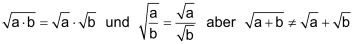
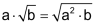
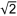 ist eine «irrationale Zahl» (nicht durch einen Bruch
ist eine «irrationale Zahl» (nicht durch einen Bruch  darstellbar).
darstellbar).