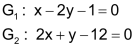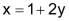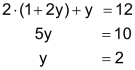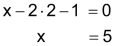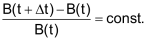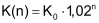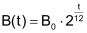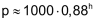Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Einheiten
|
Beim Messen von Grössen braucht man (Mass-) Einheiten als Vergleich. |
|
|
Beispiele: |
| Längen misst man z.B. in | m, dm, cm, mm, km |
| Flächen misst man z.B. in | m2, dm2, cm2, mm2, a, ha, km2 |
| Volumina misst man z.B. in | cm3, dm3, m3 – aber auch in ml oder l |
| Zeit misst man z.B. in | s, min, h |
| Massen misst man z.B. in | kg, g, mg, t |
| Geschwindigkeiten in | km/h, m/s |
| Dichten in | g/cm3, kg/m3 – aber auch in kg/dm3 |
Einsetzungsverfahren
| Verfahren zur algebraischen Lösung eines linearen Gleichungssystemes. | |
| Gegeben seien zwei Gleichungen: |
|
| Schritt 1 G1 auf x lösen. |
|
|
Schritt 2 |
|
| Schritt 3 Ergebnis in Gleichung G1 einsetzen und die Gleichung auf x lösen. |
|
| siehe auch Additionsverfahren und Gleichsetzungsverfahren | |
Entwicklungsfaktor [ zurück ]
|
Beträgt die «Wachstumsrate» r bei exponentiellem Wachstum zum Beispiel 2%, so ändert sich die betrachtete Grösse pro Zeitschritt offenbar um den konstanten Faktor 1,02. |
|
Die Zahl q = 1 + r heisst «Entwicklungsfaktor» oder «Wachstumsfaktor». Bei exponentieller Abnahme («Zerfall») ist r negativ und 0 < q < 1. |
erweitern
| Siehe Bruchoperationen |
euklidischer Algorithmus
|
Der euklidische Algorithmus beschreibt ein Verfahren, mit dem der |
| siehe Algorithmus |
eulerscher Polyedersatz
exponentieller Zerfall
| Nimmt eine Grösse in gleichen Zeitschritten um immer den gleichen Prozentsatz ab, spricht man von «exponentiellem Zerfall» oder «exponentieller Abnahme». |
|
Beispiel |
|
|
| Siehe auch radioaktiver Zerfall und Abschreibung |
exponentielles Wachstum
|
Nimmt eine Grösse B pro Zeitschritt (pro Sekunde, pro Stunde, pro Jahr, …) immer um den gleichen Prozentsatz zu, so spricht man von «exponentielles Wachstum». |
|
|
Die Wachstumsrate ist konstant: |
|
Im Koordinatensystem liegen die Punkte (t/B(t)) auf einer Kurve mit der Gleichung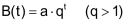 |
| Beispiele | |
|
♦ ♦ |
Kapitalentwicklung mit konstantem Zinssatz 2%: |
|
|
|
|
♦
|
Abnahme des Luftdruckes mit zunehmender Höhe: |
| siehe auch Abschreibung und Entwicklungsfaktor | |