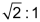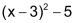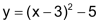Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Faktor
|
Siehe Multiplikation |
faktorisieren
| «faktorisieren» heisst «in Faktoren zerlegen». | |
| 1 | Beim Buchstabenrechnen oder bei Lösen von Gleichungen sind Ausklammern oder der Einsatz der Binomischen Formeln wichtige Techniken dazu. Umkehrung ist das Ausmultiplizieren, siehe Distributivgesetz. |
| 2 | Natürliche Zahlen, die nicht Primzahlen sind, lassen sich als Produkt darstellen. Die auftretenden Faktoren heissen Teiler der Zahl. |
| Wichtig ist die Zerlegung einer Zahl in lauter Primfaktoren, siehe Primfaktorzerlegung. | |
Fakultät
|
Drei verschiedene Objekte A, B und C kann man auf 3 ∙ 2 ∙ 1 Arten «permutieren»: Für die erste Position hat man drei Auswahlmöglichkeiten, für die zweite noch zwei und für die dritte Position bleibt bloss noch ein Objekt übrig. |
|||
|
Für n verschiedene Objekte gibt es folgende Anordnungsmöglichkeiten: |
|||
|
n ∙ (n - 1) ∙ (n - 2) ∙ 3 ∙ 2 ∙ 1 |
|||
|
Abkürzung für dieses Produkt ist der Ausdruck n! (gelesen «n Fakultät»). Seine Grösse wächst sehr schnell: |
|||
| Ein Beispiel: | |||
|
5! 10! 20! 70! |
= = = |
120 3'628'800 2,4 ∙ 1018 ergibt eine Zahl mit über 100 Stellen und überfordert auch einen gewöhnlichen Taschenrechner. |
|
| Siehe Permutation | |||
Fläche
|
Zweidimensionales Gebilde, dessen Grösse man durch Vergleich mit einer Einheitsfläche bestimmt. Oft wird die Grösse einer Fläche einfach «Fläche» genannt. |
|
Siehe auch Flächeninhalt |
Flächeneinheiten
|
Ein Quadrat mit der Seitenlänge 1 cm (das «Zentimeterquadrat») hat eine Fläche von 1 cm2, das «Meterquadrat» hat eine Fläche von 1 m2. |
|
|
Weil in einem Meterquadrat 100 · 100 Zentimeterquadrate Platz finden, |
|
| Weitere gebräuchliche Flächeneinheiten: | |
| 1 km2 | = 100 ha (Hektaren) |
| 1 ha | = 100 a (Aren) |
| 1 a | = 100 m2 |
| 1 m2 |
= 100 dm2 |
| 1 dm2 | = 100 cm2 |
Flächeninhalt
Formate
|
Schreibpapier oder Couverts sind in der Regel nur in bestimmten Grössen erhältlich. Diese «Formate» wurden durch das Deutsche Institut für Normierung (DIN) festgelegt und sind heute auch in der Schweiz gültig. |
|
Am vertrautesten ist uns das Format DIN-A. Bei allen (rechteckigen) Blättern dieses Types ist das Verhältnis der Seiten zueinander identisch: |
|
Aus einem DIN-A4-Blatt entstehen durch halbieren senkrecht zur längeren Seite zwei Blätter des Formats A5. |
 |
|
Die Fläche des Formates DIN-A0 beträgt 1m2. Somit betragen bei einem DIN-A4-Blatt die Seitenlängen etwa 210 mm bzw. 297 mm. |
Formvariable
| Variablen einer Gleichung, nach denen nicht aufgelöst wird, nennt man «Formvariablen» oder «Parameter». Die Lösung einer Gleichung mit Formvariablen hängt davon ab, welche Grössen man für die Formvariablen wählt. | |
| Beispiele | |
| ♦ ♦ |
Die quadratische Gleichung x2 + c = 0 hat nur für c < 0 jeweils zwei Lösungen. Die Funktionsgleichung y =a · (x – u)2 + v beschreibt alle quadratischen Parabeln. Erst durch die Wahl des Scheitelpunktes S (u / v) sowie des Formfaktors a wird eine ganz bestimmte Parabel definiert. |
Funktion [ zurück ]
|
Oft gibt es zwischen zwei Grössen x und y einen Zusammenhang. Ist dieser so, dass jedem x genau ein y zugeordnet werden kann, so spricht man von einer «Funktion». |
|
Die Menge aller x-Werte nennt man «Definitionsbereich» oder «Originalbereich». |
|
x heisst meist «freie» oder «unabhängige» Variable. |
|
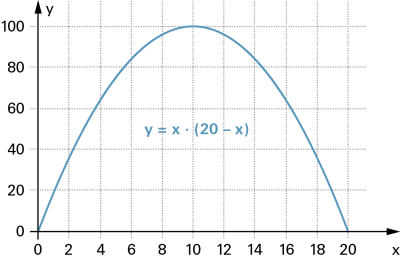
Beispielaufgabe |
|
Wertetabelle zur Aufgabe: |
Die einzelnen Wertepaare lassen sich nach folgender «Funktionsgleichung» berechnen: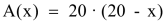 |
|
Der zugehörige Graph im Koordinatensystem zeigt die Entwicklung der Funktion (in unserem Beispiel die Entwicklung des Flächeninhaltes in Abhängigkeit von der Rechteckslänge). |
 |
|
siehe auch |
Funktionsterm
| Die Vorschrift, nach der zu einer freien Variablen der zugehörige Funktionswert berechnet wird, nennt man «Funktionsterm». |
|
Beispiel |
|
Überträg man die Wertepaare (x, y) als Punkte in ein Koordinatensystem, so liegen alle Punkte auf einer Parabel mit folgender Funktionsgleichung: |