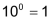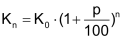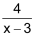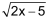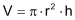Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Zahlen
|
Zahlen sind eine der bedeutendsten kulturhistorischen Erfindungen der Menschheit. Zuerst wurden Zahlen sicher zum Zählen gebraucht: 1, 2, 3, 4, … Diese Zahlen nennt man «Natürliche Zahlen». Kulturgeschichtlich kamen als Zweites die «Brüche» dazu, darauf die «Null», die für das Rechnen in einem Positionssystem unabdingbar ist. Bald wurde der Bereich der Brüche verlassen. Schon wenn man die Länge der Quadratdiagonalen sucht, verlässt man diesen Bereich: |
|
 |
Zahlengerade
|
Zahlen lassen sich der Grösse nach ordnen und geometrisch aufgereiht auf einer Geraden veranschaulichen: |
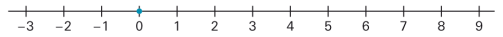 |
|
Zu jeder Zahl gehört ein bestimmter Ort auf der Zahlengeraden. |
|
Im Allgemeinen ist die Einteilung einer Zahlengeraden «aequidistant», d.h. die Zahl 2·a findet sich doppelt so weit von der Nullmarke entfernt wie die Zahl a. |
Zahlenmengen
| natürliche Zahlen | 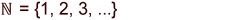 |
| ganze Zahlen | 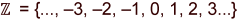 |
| negative ganze Zahlen | 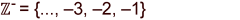 |
| rationale Zahlen |  |
| irrationale Zahlen |  |
|
|
|
Zehnerpotenz
|
Beispiele |
|||
| 1 Milliarde | = | 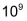 |
|
| 1 Billion | = |  |
|
| 1 Tausendstel | = | 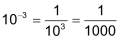 |
|
| 1 Millionstel | = | 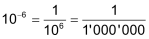 |
|
|
Beachte |
|||
|
|
|||
|
Siehe Potenzgesetze und wissenschaftliche Schreibweise |
|||
zentrische Streckung [ zurück ]
| Die (zentrische) Streckung bildet einen Punkt P von einem Zentrum Z in einen Bildpunkt P' ab. | ||
| Abbildungsvorschriften | ||
| ♦ ♦ |
P' liegt auf der Geraden g(Z,P).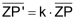 k heisst «Streckfaktor». Für k < 0 liegen Original und Bildpunkt auf verschiedenen Seiten des Streckzentrums Z. |
 |
| Eigenschaften | ||
| ♦ ♦ ♦ ♦ ♦ |
Bild und Original haben die gleiche Form (sind zueinander ähnlich). Bildstrecke und Originalstrecke sind zueinander parallel. Längen verhalten sich bei Bild und Original wie k : 1. Flächen verhalten sich bei Bild und Original wie k2 : 1. Volumina verhalten sich bei Bild und Original wie k3 : 1. |
 |
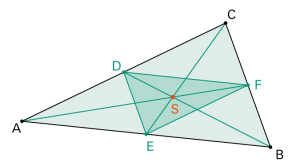
| Spezialfall Aus dem Dreieck ABC wird durch zentrische Streckung vom Schwerpunkt S aus mit k = –0,5 das Mittendreieck. |
 |
|
Zentriwinkel
| Siehe Kreiswinkelsätze |
Ziffer
|
Mit den zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9 stellen wir im Zehnersystem («Dezimalsystem») jede noch so grosse und auch jede beliebig kleine Zahl dar. |
|
3'490 = 3.103 + 4.102 + 9.101 3'492,5 = 3.103 + 4.102 + 9.101 + 2.100 + 5.10-1 |
|
Unsere Zahldarstellung ist eine Abkürzung für eine Summe von Zehnerpotenzen! |
|
Siehe auch Stellenwert-Tafel |
Zins
|
Der «Gläubiger» leiht dem «Schuldner» einen Geldbetrag B. Der Schuldner zahlt pro Jahr, in dem er beim Gläubiger in der Schuld steht, diesem einen «Zins» zu einem abgemachten Zinssatz von p%. |
|
Beispiel |
|
Für Laufzeiten von weniger als einem Jahr bezahlt man einer Bank den sogenannten «Marchzins». Er beträgt den Bruchteil (Laufzeit in Tagen : 360 Tage) vom Jahreszins. |
|
Beispiel |
| siehe auch Monatszins |
Zinseszins
|
Wird ein Kapital über mehrere Jahre angelegt und der Jahreszins immer wieder zum Kapital geschlagen, so spricht man von «Zinseszins». |
|
|
Bei einem Zinssatz von 3% beispielsweise gilt: und entsprechend |
|
|
Mit p% für den Zinssatz lautet die «Zinseszinsformel» |
Zufallsexperiment
| Man spricht von einem Zufallsexperiment, wenn der Ausgang einer Handlung vom Zufall gesteuert wird. Man kann im Einzelfall nicht voraussagen, welcher der möglichen Ausgänge (auch Ereignisse oder Ausfälle genannt) eintritt. |
zugelassene Zahlen
|
Es gibt Terme, die (zum Beispiel im Bereich der reellen Zahlen) nicht definiert sind oder keinen Sinn machen. |
|
|
Beispiele |
|
| ♦ |
|
| ♦ |
|
| ♦ | Die Gleichung x3 + y3 = z3 hat im Bereich der natürlichen Zahlen keine Lösung. Sie ist – wenn nur natürliche Zahlen zugelassen sind – unlösbar. |
|
Im Zusammenhang mit (Un-)Gleichungen oder Funktionen spricht man statt von «zugelassenen Zahlen» meist vom Definitionsbereich. |
|
Zweiersystem
| siehe Binärsystem |
Zylinder
|
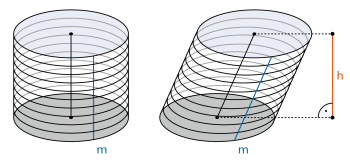
Wird ein Kreis (Grundfläche) aus der Ebene heraus in eine konstante Richtung verschoben, so überstreicht er eine Zylinderfläche. |
|
 |
|
|
Die Zylinderachse entspricht der Verbindung vom Grundflächenmittelpunkt zum Deckflächenmittelpunkt. Eine Mantellinie m verläuft auf dem Mantel parallel zur Zylinderachse. |
|
|
Für das Volumen gilt: |
|
|
|
|
|
Oft versteht man unter «Zylinder» den geraden Kreiszylinder: Die Zylinderachse steht senkrecht auf den Kreisflächen. Andernfalls heisst der Zylinder schief. |
|
|
Mantelfläche beim geraden (Kreis-) Zylinder: |
|
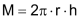 |
|
|
Siehe auch Oberfläche |
|


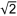 ist eine «irrationale Zahl» (nicht durch einen Bruch
ist eine «irrationale Zahl» (nicht durch einen Bruch  darstellbar).
darstellbar).