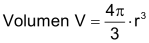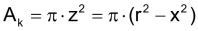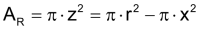Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Karat
|
Die Reinheit von Gold wurde früher in «Karat» (kt) angegeben. |
|
Heute wird die Reinheit von Gold üblicherweise in Promille angegeben. Die Stempelung «750» in einem Schmuckstück bedeutet, dass die Legierung von 1000 Gewichtsanteilen 750 Anteile (d.h. drei Viertel) reines Gold enthält. |
kartesisch
| Siehe Koordinaten |
Kathete
| Siehe rechtwinkliges Dreieck |
Kathetensatz
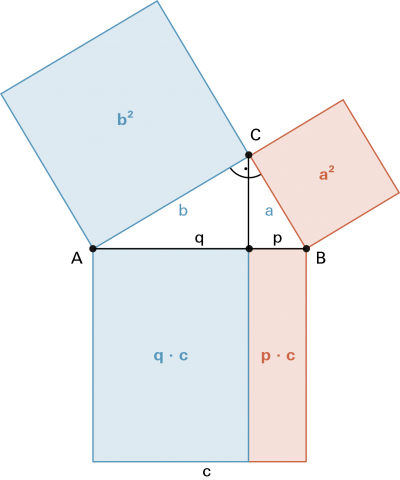
| Im rechtwinkligen Dreieck hat das Kathetenquadrat die gleiche Fläche wie das Rechteck aus dem anliegenden Hypotenusenabschnitt und der Hypotenuse. |
|
Dieser Satz wird auch «Kathetensatz des Euklid» genannt. |
|
|
Kegel
|
Ein (gerader) Kreiskegel hat als Standfläche einen Kreis. |
|
|
Kreissektor |
|
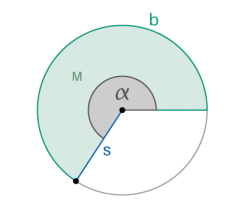 |
Bogenlänge b Mantelfläche M |
|
Grund und Aufriss des Kegels |
|
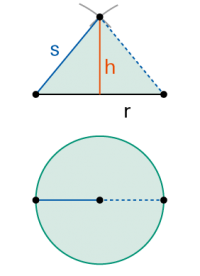 |
|
|
Schrägbild |
|
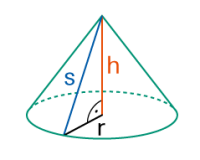 |
Volumen V Mantelfläche M |
Kegelstumpf
 |
Mantelfläche M Volumen V |
kilo-
Klammerregeln
| Siehe Rechengesetze |
Kombinatorik
|
Bei sehr vielen mathematischen Problemstellungen ist systematisches Zählen gefragt. Kombinatorik ist ein Teilgebiet der Mathematik und steht für «Kunst des Zählens». Oft hilft beim systematischen Zählen ein Baumdiagramm. |
|
Beispiel: |
|
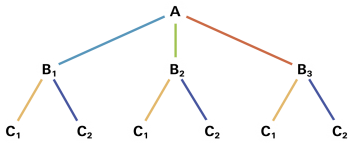
Wie viele verschiedene Wege gibt es von A über B nach C, wenn man bei A unter drei und bei B unter zwei Wegen wählen kann? |
 |
|
Aus dem Baumdiagramm ersieht man sofort, dass es 3 · 2 = 6 verschiedene Wege gibt. |
| Siehe auch Produktregel, Permutation und Lotto |
Komma [ zurück ]
|
Das Komma trennt im Dezimalsystem die Stellenwerte zwischen Einern und Zehnteln. |
|
Grafisch erfolgt diese Trennung heute oft durch einen Punkt, den «Dezimalpunkt» (Taschenrechner, Computer). |
| Siehe auch Stellenwert |
Kommutativgesetz
| Siehe Rechengesetze |
konformer Zinssatz
| siehe Monatszins |
kongruent
|
Zwei Objekte sind «kongruent», wenn sie die gleiche Form und die gleiche Grösse haben. |
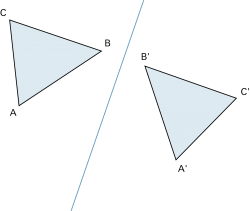
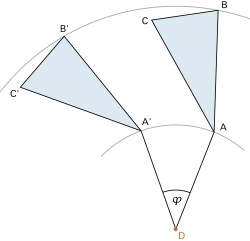
Kongruenzabbildung
|
Eine Kongruenzabbildung führt eine Figur in eine gleich grosse Figur von gleicher Form über. Dabei bleiben Winkel, Längen und Flächen der Figur unverändert. |
|
|
Die Achsenspiegelung, die Drehung, die Punktspiegelung und auch die Schiebung sind Kongruenzabbildungen. |
|
|
Achsenspiegelung: |
Drehung: |
Punktspiegelung: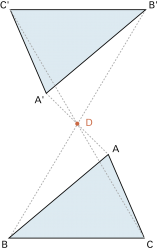 |
Schiebung: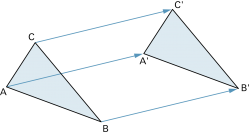 |
Kongruenzsätze
|
Dreiecke sind kongruent, wenn sie in drei (geeigneten) Stücken übereinstimmen. |
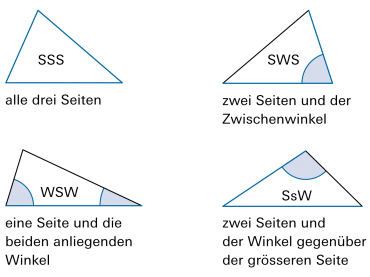 |
|
Das heisst auch: Wenn die drei Stücke vorgegeben werden, ist das Dreieck in Grösse und Form vollständig bestimmt. |
konvex
|
Ein Vieleck ohne einspringende Ecken wird «konvex» genannt. |
|
 konvexes Vieleck |
 nicht konvexes Vieleck |
|
Allgemein |
|
Koordinaten
 |
|
Legt man in die Ebene ein (kartesisches) Koordinatensystem, gehört zu jedem Punkt in eindeutiger Weise ein Zahlenpaar P(x/y). |
|
Normalerweise wählt man die x-Achse horizontal mit Richtungspfeil nach rechts (rot in der Abbildung), die y-Achse vertikal mit Richtungspfeil nach oben (blau in der Abbildung). |
|
Die erste Koordinate eines Punktes ist die x-Koordinate, die zweite Koordinate eines Punktes ist die y-Koordinate. |
|
Um die Lage eines Punktes im Raum eindeutig festzulegen, benutzt man drei paarweise aufeinander senkrecht stehende Achsen. Jeder Raumpunkt ist dann durch drei Koordinaten P(x/y/z) eindeutig festgelegt. |
Koordinatensystem
|
Ein Koordinatensystem ist ein Raster, das die Ebene (oder den Raum) so in genau lokalisierbare Teile zerlegt, dass die Lage eines Punktes, einer Geraden, einer Ebene oder eines Graphen durch eine Vorschrift (Zahlen, Gleichung) eindeutig auszumachen ist. |
| Siehe auch Koordinaten. |
Koordinatensystem, dreidimensional
|
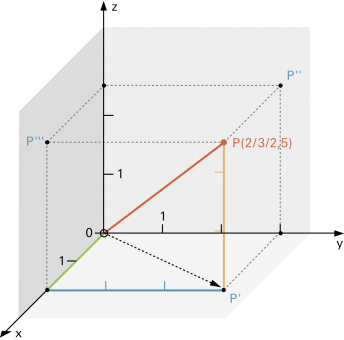
Um die Lage eines Punktes im Raum eindeutig festzulegen, kann man ein «kartesisches Koordinatensystem» einsetzen (die drei Achsen x, y und z stehen paarweise senkrecht aufeinander). |
 |
|
Den Punkt P (2/3/2,5) erreicht man vom Koordinatenursprung her, indem man sich 2 Schritte in x-Richtung, 3 Schritte in y-Richtung und dann 2,5 Schritte in z-Richtung bewegt. |
|
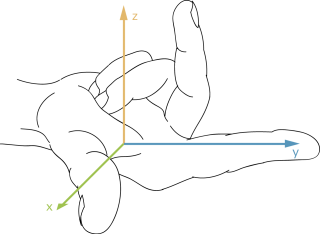
Das kartesische Koordinatensystem wird normalerweise als Rechtssystem bzw. rechthändiges System dargestellt: Daumen, Zeigfinger und Mittelfinger der rechten Hand zeigen in dieser Reihenfolge in x-, y- und in z-Richtung. |
 |
Kreisdiagramm
|
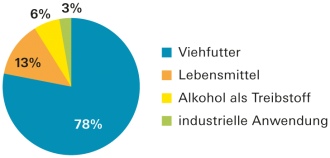
Im Kreisdiagramm (auch «Tortendiagramm» genannt) werden Anteile an einem Ganzen dargestellt. |
 |
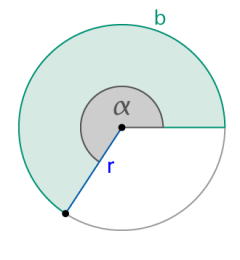
Kreissektor
|
|
Sektorfläche As damit gilt für die Sektorfläche auch |
Kreistangente
|
Von einem Punkt P ausserhalb eines Kreises gibt es zwei Tangenten an den Kreis. |
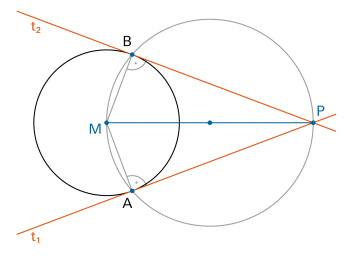 |
|
Siehe auch Kreisteile |
Kreisteile
|
Linien und Flächen am Kreis: |
 |
Kreiswinkelsätze
|
Für jeden Punkt C auf dem Bogen über AB gilt: Der zugehörige Peripheriewinkel (auch «Umfangswinkel» genannt) ist halb so gross wie der zugehörige Zentriwinkel: |
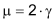 |
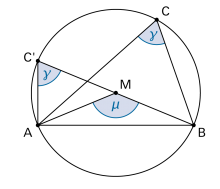 |
|
Im Grenzfall |
|
Siehe Satz des Thales |
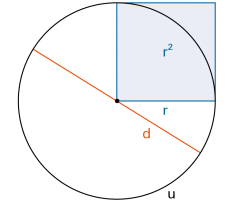
Kreiszahl π
Die Kreiszahl π ist eine Verhältniszahl. Sie tritt entweder als Verhältnis von  oder auch von oder auch von 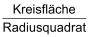 auf. auf. |
||
 |
||
|
π ist eine irrationale Zahl. Als Dezimalbruch dargestellt bricht π nicht ab und ist nicht periodisch. Gerundet auf 5 Stellen: π ≈ 3,14159 |
||
| Damit gilt für die Kreisfläche | AKreis = π ∙ r 2 | |
| und für den Kreisumfang | uKreis = 2π ∙ r = π ∙ d | |
|
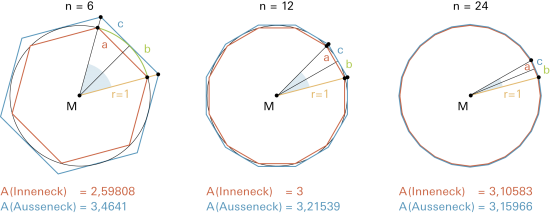
Ist ein Kreis Umkreis eines regulären n-Ecks und zugleich Inkreis eines regulären n-Ecks, kann seine Fläche durch Einschachteln mit wachsendem n immer genauer bestimmt werden. Man erhält so jeweils bessere Werte für π. |
||
 |
||
| Als Mittelwerte ergeben sich auf diesem Weg hier 3,03109, 3,10765 und 3,13275. | ||
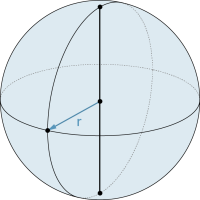
Kugel
|
||||||
|
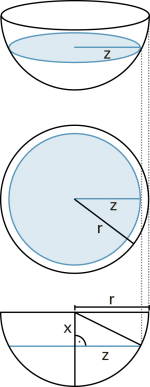
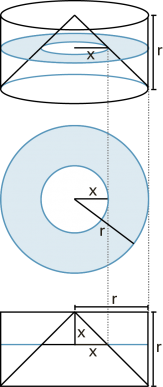
Das Prinzip von Cavalieri erlaubt die Herleitung der Fomel für das Kugelvolumen. Nach Segner sind die Querschnittsflächen einer Halbkugel und des Differenzkörpers aus Zylinder und Kegel mit Höhe h = r auf jeder Höhe gleich gross. |
||||||
|
kürzen
| Siehe Bruchoperationen |


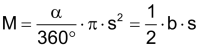
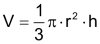
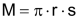
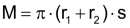
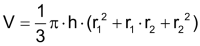
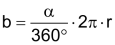
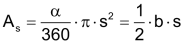
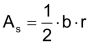

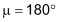 , in dem die Sehne AB zum Durchmesser wird, beträgt der
, in dem die Sehne AB zum Durchmesser wird, beträgt der