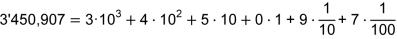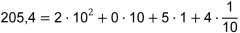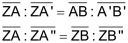Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
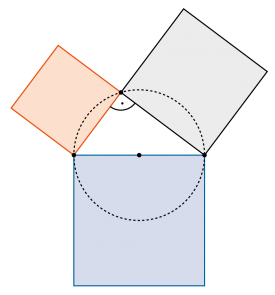
Satz des Pythagoras
|
Im rechtwinkligen Dreieck ist die Summe der beiden Kathetenquadrate gleich gross wie die Fläche des Hypotenusenquadrats. |
 |
|
Wichtig ist auch die Umkehrung des Satzes: |
| siehe auch Höhensatz und Kathetensatz |
Satz des Thales
|
Der Winkel gegenüber einem Kreisdurchmesser, welches ein Dreieck mit einem Punkt auf den Kreis bildet, beträgt 90° (rechter Winkel). |
 |
|
Anders betrachtet: Der geometrische Ort aller Punkte, von denen aus eine vorgegebene Strecke |
|
Siehe Kreiswinkelsätze |
Säulendiagramm
| Siehe Balkendiagramm |
Scheitelpunkt
| siehe quadratische Funktion |
Scheitelpunktsform
| siehe quadratische Funktion |
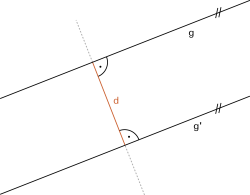
Scheitelwinkel
| siehe Winkel an Geraden |
Schiebung
|
Wird eine Figur in eine bestimmte Richtung als Ganzes um eine bestimmte Strecke verschoben (Pfeil in der Abbildung), so spricht man von einer «Schiebung». |
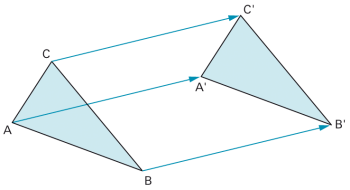 |
| Die Schiebung ist eine Kongruenzabbildung. |
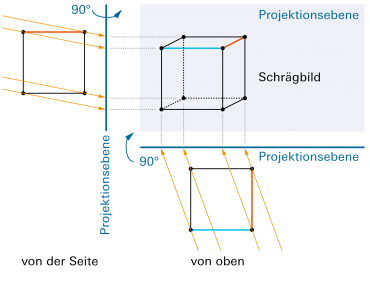
Schrägbild
|
Wenn parallele Lichtstrahlen ein Objekt – zum Beispiel einen Würfel – beleuchten, so erzeugen sie auf einem Blatt ein ebenes (zweidimensionales) Bild. Man spricht von einem «Schrägbild», wenn die Strahlen schräg (d.h. in einem Winkel von |
|
 |
|
| Für Schrägbilder gilt: | |
| ♦ | Kanten, die parallel zur Bildebene stehen, haben im Bild die Originallänge. Winkel zwischen ihnen werden nicht verändert. |
| ♦ | Parallele Kanten sind auch im Schrägbild parallel. |
| ♦ | Mitte bleibt Mitte. |
| ♦ | Kanten senkrecht zur Bildebene werden alle um den gleichen Faktor verkürzt, z.B. auf zwei Drittel ihrer Originallänge. Meist wird das Bild am anschaulichsten, wenn eine Verkürzung auf etwa die Hälfte erfolgt. |
Schwerlinie
| Die Seitenhalbierende wird auch «Schwerlinie» genannt. |
| Siehe Linien im Dreieck |
Schwerpunkt
|
Im Dreieck ist dies der Schnittpunkt der drei Seitenhalbierenden (auch Schwerlinien genannt). Der Schwerpunkt teilt die Seitenhalbierenden im Verhältnis 2 : 1. |
| Im Allgemeinen unterscheidet man bei ebenen Figuren zwischen einem Ecken-Schwerpunkt und einem Flächen-Schwerpunkt. Beim Dreieck fallen der Ecken-Schwerpunkt und der Flächen-Schwerpunkt zusammen. |
| Siehe auch Linien im Dreieck |
Segment
| Siehe Kreisteile |
Sehne
| Siehe Kreisteile |
Sehnenviereck
|
Ein Viereck mit Umkreis heisst Sehnenviereck. |
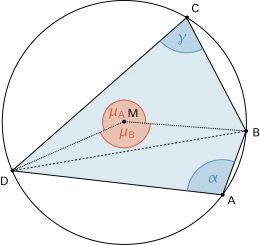 |
|
Im Sehnenviereck sind gegenüberliegende Winkel zusammen 180° gross, weil die zugehörigen Zentriwinkel sich auf 360° ergänzen. |
| Siehe auch Kreiswinkelsätze |
Seitenhalbierende im Dreieck
| Verbindung einer Dreiecksecke mit der Mitte der gegenüberliegenden Seite. Sie teilt das Dreieck in zwei flächengleiche Teildreiecke. |
| Siehe auch Linien im Dreieck |
Seitenmittendreieck
| Siehe Mittendreieck |
Sekante
| Siehe Kreisteile |
Sektor
| Siehe Kreisteile |
senkrecht
|
Wenn Geraden oder Strecken einen 90°-Winkel bilden, spricht man von «senkrecht stehen». |
 |
|
Gebräuchlich sind die beiden Darstellungen oben. |
|
Eine Gerade kann im Raum senkrecht auf einer Ebene stehen (man spricht auch vom «Lot auf einer Ebene»), und ebenso kann eine Ebene auf einer anderen Ebene senkrecht stehen: |
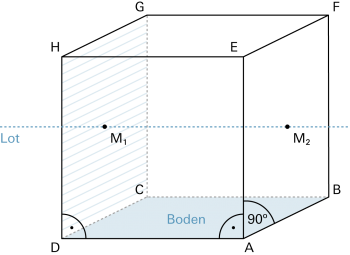 |
|
Die Strecke |
|
Die Ebene links durch die Seitenfläche DCGH steht senkrecht auf der Bodenebene ABCD. Die Gerade durch die Flächenmitten M1 und M2 steht senkrecht auf der Seitenfläche DCGH. |
SI-Einheiten
| Das Kürzel «SI» steht für «Système International d'Unités». | ||||
| Dahinter steckt eine internationale Vereinbarung zu den Masseinheiten. Grundgrössen werden festgelegt und physikalisch möglichst exakt definiert. | ||||
| Grundgrösse Länge Masse Zeit elektr. Stromstärke Temperatur |
Symbol l m t I T |
Grundeinheit Meter Kilogramm Sekunde Ampère Kelvin |
Abkürzung m kg s A K |
|
| Aus den Grundeinheiten bildet man die abgeleiteten Einheiten wie Joule (J) für die Energie, Watt (W) für die Leistung, Newton (N) für die Kraft, Hertz (Hz) für Frequenzen usw. | ||||
Stabdiagramm
|
Statt mit Rechtecken wie im Balkendiagramm werden Werte im Stabdiagramm durch vertikale Strecken dargestellt. |
Statistik
|
In der Statistik werden Daten gesammelt, dargestellt und ausgewertet (interpretiert). Statistik ist ein wesentliches Hilfsmittel in Naturwissenschaften, Soziologie, Ökonomie, Meteorologie, Medizin, Politik, Technik usw. und somit nicht mehr aus dem Alltag wegzudenken. |
Daten können in Tabellen oder als Grafiken dargestellt werden.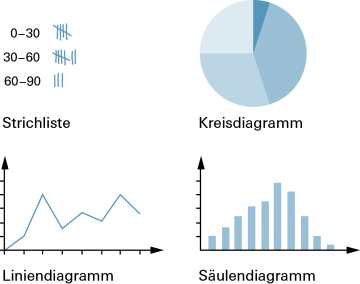 |
|
Von einer statistischen Untersuchung werden oft bloss wenige charakteristische Zahlen bekannt gegeben, zum Beispiel das arithmetische Mittel oder der Median. |
|
Hinweis Die einprägsame Darstellung mittels Bildern birgt in sich die Gefahr der Manipulation. Beim Interpretieren von Grafiken muss man deshalb besonders auf die ausgewählten Achsenabschnitte und auf eventuell verzerrte Achsenmassstäbe achten. |
Steigung
|
Bei einem Keil, einer Rampe, aber auch bei einer Geraden im Koordinatensystem ist die Steigung definiert als Verhältnis |
| Im Alltag spricht man auch von Gefälle statt von Steigung, wenn es abwärts geht. Bei der Geraden im Koordinatensystem hat die Steigung dann einen negativen Zahlenwert. |
 |
|
Zu einem Steigungswinkel von 45° gehört die Steigung 1 = 100% |
|
Siehe auch Geradengleichung |
Stellenwert
Stichprobe
|
Will man zur Wirksamkeit eines Medikamentes, zur Höhe der Wohnungsmieten in einer Stadt, zur Lebensdauer eines bestimmten Lampentyps, zum voraussichtlichen Ausgang einer Wahl, zu den Fernsehgewohnheiten von Jugendlichen in der Schweiz, … eine Auskunft haben, so zieht man aus dem zu untersuchenden Bereich eine «Stichprobe». |
|
An der Stichprobe führt man dann die notwendigen Untersuchungen durch und versucht aus den Resultaten eine verlässliche Aussage über die Grundmenge zu machen. |
Strahlensätze
|
Wird ein Dreieck AZB durch zentrische Streckung abgebildet, stehen auftretende Streckenlängen auf den Parallelen (in der Illustration blau) und den beiden Geraden |
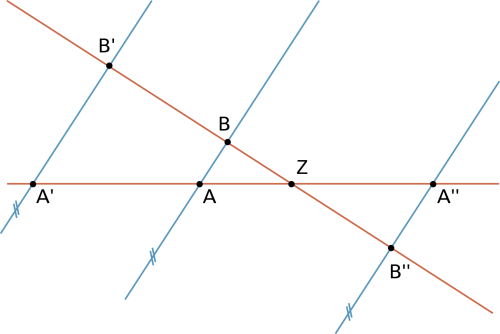 |
|
Beispiele
|
Streckenprofil
|
Ein Streckenprofil veranschaulicht grafisch einen Weg so, dass horizontal die Distanz zum Startpunkt und vertikal je die zugehörige Höhe über Meer (in überhöhtem Massstab) aufgetragen wird. |
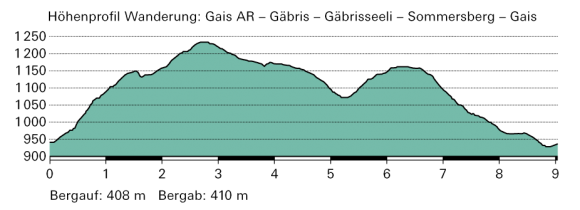 |
Streckenteilung
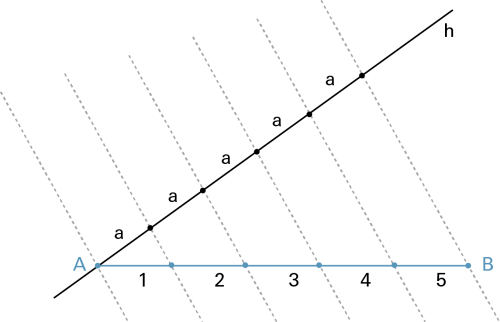
|
Wir zeigen die Teilung einer Strecke AB in n gleiche Teile am Beispiel von n = 5. |
|
Eine Hilfsgerade h wird durch den Anfangspunkt A gelegt. Dann werden auf dieser Geraden n gleich lange Strecken abgetragen. |
Streckfaktor
| siehe zentrische Streckung |
Streifenbreite
Strichoperation
|
Addition und Subtraktion heissen «Strichoperationen», weil ihre Operationszeichen durch Striche dargestellt werden (Operationen erster Stufe). |
| Siehe auch Punkt vor Strich |
Stufenwinkel
| siehe Winkel an Geraden |
subtrahieren
| Subtrahieren heisst «abzählen». |
| Siehe Subtraktion |
Subtraktion
| Die Subtraktion ist die Umkehroperation der Addition und somit eine Operation erster Ordnung. Das Operationszeichen ist das – («Minus»). | |||
| Eine Differenz ist … | |||
| a) | das Ergebnis einer Subtraktion: | ||
| 23 − 8 = 15 | |||
| oder | |||
| b) | der (nicht ausgerechnete) Term mit dem Minuszeichen als Hauptzeichen: | ||
|
23 − 8 3a − b (3a + b) − 2a |
|||
|
Siehe auch Rechengesetze |
|||
Symmetrieachse [ zurück ]
|
siehe Achsenspiegelung |
Symmetriezentrum
|
siehe Punktspiegelung |


 unter einem rechten Winkel erscheint, ist der «Thaleskreis» über
unter einem rechten Winkel erscheint, ist der «Thaleskreis» über  steht senkrecht auf der Bodenebene ABCD. Die gleiche Strecke steht auch senkrecht auf der Strecke
steht senkrecht auf der Bodenebene ABCD. Die gleiche Strecke steht auch senkrecht auf der Strecke  und auf der Strecke
und auf der Strecke  .
. .
.