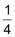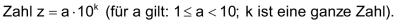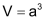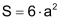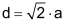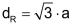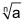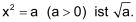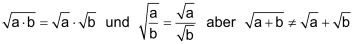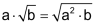Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Wachstumsfaktor
Wahrscheinlichkeit
|
Wahrscheinlichkeiten sind Prognosen für die relative Häufigkeit, mit der ein bestimmtes Ereignis bei einem Zufallsexperiment eintritt. |
|||
|
Als Platzhalter für Wahrscheinlichkeitswerte wird meist der Buchstabe p («probability») gewählt. Für p gilt immer 0 ≤ p ≤ 1, d.h. der Wert für eine Wahrscheinlichkeit ist nie kleiner als 0 und nie grösser als 1. |
|||
|
• • • |
Tritt ein Ereignis mit Sicherheit ein, so ist p = 1. Ein unmögliches Ereignis hat die Wahrscheinlichkeit p = 0. In allen anderen Ereignissen ist p grösser als 0 und kleiner als 1. |
||
|
Aufgrund von wiederholten Experimenten oder auch von Symmetrieüberlegungen sind Voraussagen über die Grösse von p möglich. |
|||
|
Besonders einfach ist die Berechnung der Wahrscheinlichkeit dann, wenn alle Möglichkeiten gleich wahrscheinlich sind. Dann rechnet sich die Wahrscheinlichkeit nach folgender Formel: |
|||
 |
|||
|
Diese Formel wird «Laplace-Formel» genannt. |
|||
|
Beispiel 1 |
|||
|
Bei einem Würfel treten im Mittel alle Augenzahlen mit gleicher relativer Häufigkeit auf, damit ist die Wahrscheinlichkeit… |
|||
|
• |
eine 6 zu werfen |
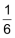 |
|
| • | eine gerade Augenzahl zu werfen | 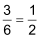 |
|
|
Beispiel 2 |
|||
|
Wirft man eine Münze zweimal hintereinander, so sind die möglichen Ergebnisse Dabei ist die Wahrscheinlichkeit für … |
|||
|
• |
zweimal Kopf |
|
|
| • | einmal Kopf und einmal Zahl | 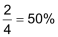 |
|
Wahrscheinlichkeitsbaum
|
In mehrstufigen Zufallsversuchen gibt oft ein Baumdiagramm eine gute Übersicht. Darin werden die Ausfälle und die zugehörigen Wahrscheinlichkeiten eingetragen. |
|
Beispiel |
|
Doppelwurf mit einem fairen Würfel: |
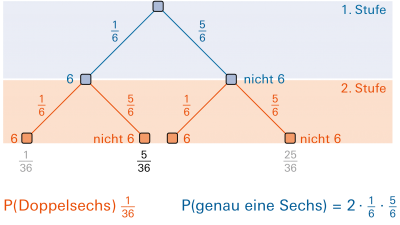 |
Wanderungsgewinn
|
Als «Wanderungsgewinn» bezeichnet man die Differenz zwischen der Anzahl Personen, die innerhalb eines Jahres in ein Land einwandern und der Anzahl Personen, die das Land verlassen. |
Wechselkurs
|
Der Wechselkurs ist der Preis einer Währung ausgedrückt in einer anderen Währung. |
|
|
Ankauf: Verkauf: |
Die Bank kauft meine Euros zu CHF 1.18 pro € Die Bank verkauft mir Euros zu CHF 1.22 pro € |
|
Die Ausdrücke «Ankauf» und «Verkauf» sind jeweils aus der Optik der Bank zu verstehen: |
|
Wechselsumme
|
Prüfkriterium für die Teilbarkeit einer Zahl durch 11. |
|||
|
Die Wechselsumme muss eine 11er-Zahl sein. |
|||
|
Wechselsumme bilden: |
|||
|
w = E ∙ 1 + Z∙ (–1) + H ∙ 1 + T ∙ (–1) + ∙∙∙ |
|||
|
(E ist die Einer-, Z die Zehnerziffer, H die Hunderterziffer etc.) |
|||
|
Beispiel: |
|||
|
z = 1'171'709 |
|||
|
→ Wechselsumme w = 9 ∙ 1 + 0 ∙ (–1) + 7 ∙ 1 + 1 ∙ (–1) + 7 ∙ 1 + 1 ∙ (–1) + 1 ∙ 1 = 22 |
|||
|
Beim Teilen von w durch 11 bleibt Rest 0, also ist auch z teilbar durch 11. |
|||
Wechselwinkel
| siehe Winkel an Geraden |
Wertetabelle
|
Zusammenhänge zwischen Grössen können in einer Wertetabelle festgehalten werden. Beispiel: |
| Menge [g] | 100 | 200 | 300 | 400 | 500 | 600 |
| Preis [CHF] | 3.00 | 6.00 | 9.00 | 15.00 | 22.50 | 30.00 |
| Die Wertepaare (Menge/Preis) lassen sich dann im Koordinatensystem anschaulich als Graph darstellen. |
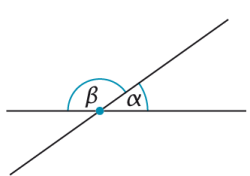
Winkel an Geraden
|
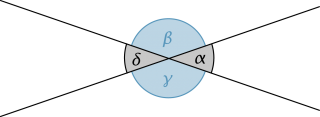
Zwei sich schneidende Geraden bilden vier Winkel. |
 |
|
Zwei einander gegenüberliegende Winkel heissen «Scheitelwinkel». |
|
Zwei benachbarte Winkel heissen «Nebenwinkel». |
| «Stufenwinkel» an geschnittenen Parallelen sind gleich gross: α = β. «Wechselwinkel» an geschnittenen Parallelen sind gleich gross: δ = γ. 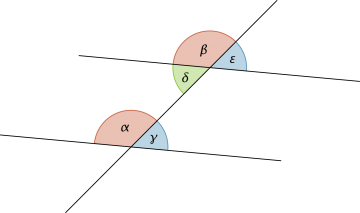 |
| siehe auch Winkelbezeichnungen |
Winkelbezeichnungen [ zurück ]
|
|
Winkelhalbierende
Winkelhalbierende im Dreieck
| Die drei Winkelhalbierenden eines Dreiecks schneiden sich in einem Punkt – dem Inkreismittelpunkt. |
| Siehe Linien im Dreieck |
Winkelsumme
wissenschaftliche Schreibweise
|
In der Wissenschaft werden sehr gross oder sehr kleine Zahlen in folgender Form angegeben: |
|||
|
|
|||
|
Beispiele |
|||
|
für |
3'500'000'000 |
schreibt man |
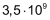 |
| für | 6'000'000'000'000'000'000 | schreibt man | 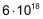 |
| für | 0,000'000'204 | schreibt man | 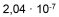 |
|
Die wissenschaftliche Schreibweise ist bei betragsmässig sehr grossen und sehr kleinen Zahlen sehr übersichtlich. Bei der Angabe von Messresultaten wählt man mit Vorteil ebenfalls die wissenschaftliche Schreibweise. Die Anzahl der Ziffern im Faktor a gibt dann Auskunft über die Genauigkeit der Messung. |
|||
|
Siehe auch Zehnerpotenzen |
|||
Würfel
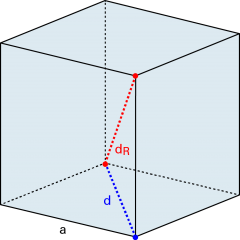
| Der Würfel ist ein platonischer Körper mit vielen speziellen Eigenschaften. | ||||||||
 |
||||||||
|
||||||||
|
Ein Würfel besitzt je mehrere zwei-, drei- und vierzählige Symmetrieachsen. |
||||||||
 |
Würfelnetz
|
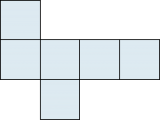
Mit «Würfelnetz» bezeichnet man sechs zusammenhängende Quadrate, die so angeordnet sind, dass daraus ein Würfel gefaltet werden kann. |
||
|
Zwei «Sechslinge», die zu einem Würfel gefaltet werden können:
|
||
|
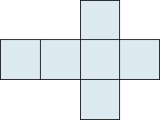
Nicht alle Anordnungen von sechs Quadraten lassen sich zu einem Würfel falten. |
||
|
Ein «Sechsling», aus dem kein Würfel gefaltet werden kann: 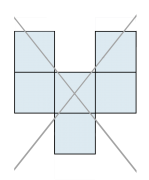 |
||
| Es gibt insgesamt 11 unterschiedliche Würfelnetze (Spiegelungen und Drehungen nicht mitgezählt). |
Wurzel
|
Die positive Lösung der Gleichung xn = a (a > 0) wird als «n-te Wurzel aus a» bezeichnet und folgendermassen geschrieben: |
|
Beispiel |
|
Die positive Lösung der Gleichung |
|
Aus den Potenzgesetzen ergibt sich, dass für positive Zahlen die beiden Ausdrücke |
|
Damit gelten für das formale Rechnen mit Wurzeln die gleichen Regeln wie beim Nützlich ist oft (in beide Richtungen!) |
| siehe Potenzgesetze |