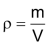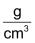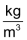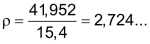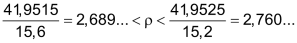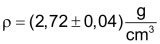Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
dezi-
Dezimalbruch
|
Zahlen mit Komma oder Punkt heissen im Zehnersystem «Dezimalbruch». |
|
Beispiele für Dezimalbrüche: |
| abbrechend | 0,45 | 0,714285 |
| periodisch |
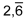 |
(gelesen: «zwei Komma Periode 6») |
| gemischt periodisch |
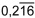 |
(gelesen: «null Komma zwei Periode eins sechs») |
|
Jeder Bruch kann auch als Dezimalbruch dargestellt werden. |
||
|
Bemerkung: |
||
|
Irrationale Zahlen können nicht als Bruch dargestellt werden. |
||
|
Beispiele: |
||
 |
||
Dezimalpunkt
|
Siehe Komma und Dezimalbruch |
Dezimalsystem
| Das Dezimalsystem ist ein Stellenwert- oder Positionssystem: Der Wert einer Ziffer hängt von ihrer Position innerhalb einer Zahl ab. Man spricht daher vom «Stellenwert» einer Ziffer. |
 |
|
Beispiel: |
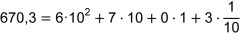 |
| Die Ziffer 6 hat in dieser Zahl den Stellenwert 6 ⋅ 102 = 600 |
| In Mesopotamien wurden Zahlen in Positionssystemen mit Basis 12 oder 60 gebraucht. Das Positionssystem mit Basis 12 hat sich bei uns in Mengenangaben wie «ein Duzend» oder «ein Gros» mit 144 (= 122) Stück gehalten; das System mit Basis 60 findet sich noch in unserer Zeiteinteilung mit 1h = 60 Minuten = 3'600 Sekunden (= 602). |
| In der Technik ist das Zweiersystem (auch «Binärsystem») von zentraler Bedeutung, weil dort mit zwei Zuständen (1 oder 0 für «Strom» oder «kein Strom») gearbeitet wird. |
| In der elektronischen Datenverarbeitung ist – neben dem Zweiersystem – ebenfalls das «Hexagesimalsystem» (Basis 16) gebräuchlich. |
| Das römische Zahlensystem ist kein Stellenwertsystem. Es eignet sich zwar zur Darstellung einer Zahl, damit zu rechnen ist aber praktisch unmöglich. |
Diagonale [ zurück ]
Diagramm
|
Eine Darstellung, die grafisch den Zusammenhang zwischen zwei oder mehr Grössen veranschaulicht, nennen wir «Diagramm». |
|
Gebräuchliche Diagrammtypen: |
|
Von einem «Diagramm» spricht man auch, wenn die Abhängigkeit zweier Grössen in einem |
Dichte
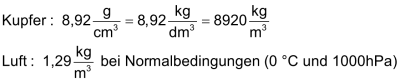
|
Die Dichte ist definiert als Verhältnis zwischen Masse und Volumen: Die Dichte wird mit dem griechischen Buchstaben
Im Alltag sind folgende Masseinheiten gebräuchlich: |
|||
|
Beispiel |
|||
 |
Differenz
|
Siehe Subtraktion |
Distributivgesetz
|
Siehe Rechengesetze |
Division
|
Die Division ist eine Operation zweiter Ordnung. |
||
|
Das Operationszeichen ist der Doppelpunkt : («durch» oder «geteilt durch», in speziellen Fällen auch «gemessen mit»); manchmal wird dafür auch ein Bruchstrich eingesetzt. |
||
|
Ein Quotient ist … |
||
| a) | das Ergebnis einer Division: | |
 |
||
| oder | ||
| b) | der (nicht ausgerechnete) Term, der von einem Durchzeichen (oder einem Bruchstrich) «zusammengehalten» wird: | |
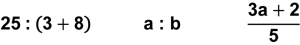 |
||
|
Die Umkehroperation der Division ist die Multiplikation. |
||
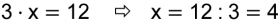 |
||
|
Damit ist eine Division durch 0 nicht erlaubt, denn dann müsste die Gleichung |
||
|
Siehe auch Bruchoperationen |
||
Doppelrechnung
| Wird eine Grösse durch Messung von mehreren Teilgrössen bestimmt – zum Beispiel eine Dichte durch Messen von Volumen und Masse – ist genau abzuklären, wie sich die Messgenauigkeiten (mögliche «Messfehler») auf das Schlussresultat auswirken. Ein praktisches Verfahren hierzu ist die «Doppelrechnung». | |
| Zuerst überlegt man sich, in welche Richtung jedes einzelne Messresultat die Schlussgrösse beeinflusst. Dann wählt man – je nachdem – den kleinstmöglichen oder den grösstmöglichen Wert der einzelnen Messresultate und setzt diese in die Formel für die Schlussgrösse ein. So erhält man eine obere und eine untere Schranke für das (Schluss-)Resultat und gleichzeitig Informationen zur Anzahl der gültigen Ziffern. | |
|
Beispiel |
|
|
♦
|
Im Schullabor wird die Masse m eines Aluminiumstücks mit einer Präzisionswaage ausgemessen. Die Waage zeigt 41,952 g – auf Milligramm genau, d.h. ± 0,0005. Unterer und oberer Wert im Rahmen der Messgenauigkeit: 41,9515 g < m < 41,9525 g |
| ♦ | Das Volumen V wird via Eintauchen bestimmt auf 15,4 cm3 – die Messgenauigkeit beträgt ± 0,2 cm3. Unterer und oberer Wert im Rahmen der Messgenauigkeit: 15,2 cm3 < V < 15,6 cm3 |
| ♦ |
Mit den gemessenen Werten wird nun die Dichte ρ berechnet.
Unterer und oberer Wert der Dichte im Rahmen der Messgenauigkeit:
Eine vernünftige Angabe des Messresultates mit (Maximal-) Fehler ist dann
|
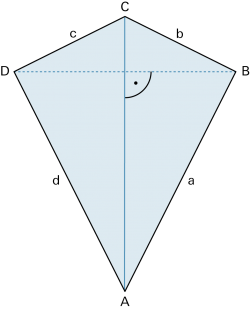
Drachenviereck
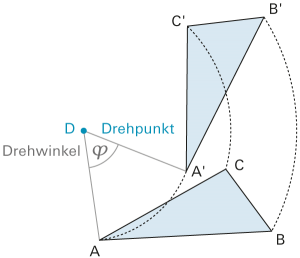
Drehung
 |
|
Die Drehung ist eine Kongruenzabbildung. |
|
Spezialfall: |
Dreieck
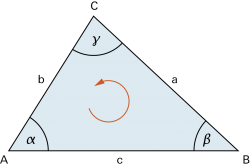
| 1 |
In einem Dreieck werden die Eckpunkte üblicherweise im Gegenuhrzeigersinn mit Grossbuchstaben in alphabetischer Reihenfolge beschriftet, zum Beispiel mit A, B, C. Die Seiten bezeichnet man dann meistens mit den entsprechenden Kleinbuchstaben a, b, c, wobei a der Ecke A gegenüberliegt, b der Ecke b und c der Ecke C. Der Winkel bei Punkt A heisst dann α («Alpha»), der Winkel bei B heisst β («Beta») und derjenige bei C heisst γ («Gamma»). |
||||||||||||||||
|
|
|||||||||||||||||
| 2 |
Dreiecke kann man nach Winkelgrössen oder Seitenlängen einteilen. Die längste Seite liegt immer dem grössten Winkel gegenüber. |
||||||||||||||||
|
|||||||||||||||||
|
|
|
||||||||||||||||
|
3 |
Der Flächeninhalt ist beim Dreieck halb so gross wie das Produkt aus einer Seitenlänge und der Länge der zugehörigen Höhe. | ||||||||||||||||
 |
|||||||||||||||||
Dualsystem
| siehe Binärsystem |
Durchschnittswert
|
siehe Mittelwerte |



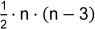 Diagonalen. Ein Sechseck hat somit neun, ein Fünfeck fünf Diagonalen.
Diagonalen. Ein Sechseck hat somit neun, ein Fünfeck fünf Diagonalen.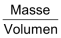
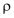 («Rho») bezeichnet:
(«Rho») bezeichnet: