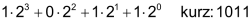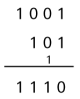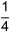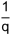Lexikon
Das Lexikon erläutert die mathematischen Begriffe aus allen Jahrgangsbänden.
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Balkendiagramm
| Balkendiagramme werden oft zur Darstellung von relativen oder absoluten Häufigkeiten eingesetzt. Die Anteile werden durch stehende, manchmal auch durch liegende Balken dargestellt. |
|
Beispiel 1: «relative Häufigkeit» |
|
Prozentualer Anteil an Haushalten mit 1, 2, 3, 4 oder 5 Personen |
 |
|
Beispiel 2: «absolute Häufigkeit» |
|
Anzahl Anhänger von blau, rot oder grün, welche die Kandidatinnen A bis D gewählt haben |
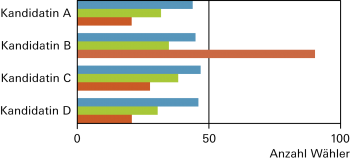 |
| Ein Diagramm wie in Beispiel 1 wird oft auch «Säulendiagramm», «Stabdiagramm» oder «Histogramm» genannt. |
Baumdiagramm
| Mehrstufige Prozesse können durch ein Baumdiagramm veranschaulicht werden. |
| Beispiel: |
| Alle möglichen Wege von Ort A nach C über Ort B. |
|
|
| Speziell wichtig sind Baumdiagramme als Hilfsmittel beim Berechnen von Wahrscheinlichkeiten und in der Kombinatorik. |
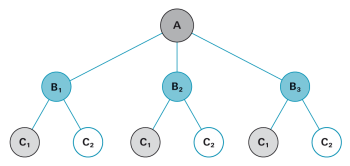
| Beispiel: |
|
Verteilung von Knaben und Mädchen in einer Familie mit drei Kindern (Geburtenfolge). |
 |
|
Es sind 8 Fälle möglich. Wenn es bei der Berechnung der Wahrscheinlichkeit um die Anzahl Mädchen geht, dann sind bloss noch 4 verschiedene Fälle zu unterscheiden: 0, 1, 2 oder 3 Mädchen. |
| Siehe auch Wahrscheinlichkeitsbaum |
Bildfigur
|
Bei einer Abbildung (z.B. einer Spiegelung) werden Figuren in ihrer Lage verändert – manchmal auch in ihrer Grösse und Form. |
|
Die Ausgangsfigur nennt man «Original», die resultierende Figur heisst «Bild» oder «Bildfigur». |
Binärsystem
|
Das Binärsystem wird auch «Dualsystem» oder «Zweiersystem» genannt. Im Zehnersystem stellen wir jede noch so grosse Zahl mit zehn verschiedenen Ziffern dar. Dualzahlen werden im Informatikbereich eingesetzt, weil ein System oft durch zwei Zustände – nämlich «1» (ein) oder «0» (aus) – beschrieben werden kann. |
|
An die Stelle der Zehnerpotenzen treten die Zweierpotenzen als Stufenzahlen: |
|
Bei der Addition zweier Zahlen werden nicht die Zehner, sondern die Zweier übertragen: |
binomische Formeln
|
Eine wichtige Rolle beim Faktorisieren von Summen haben die drei Binomischen Formeln. Ihre Bedeutung geht aber weit über dies hinaus. Der Name deutet auf zweiteilige Summen (lateinisch «bi» für «zweimal»). |
|
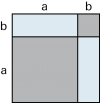
| Formel 1 (a + b)2 = a2 + 2ab + b2 | |
| geometrische Deutung: | |
 |
|
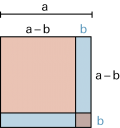
| Formel 2 (a – b)2 = a2 – 2ab + b2 | |
| geometrische Deutung: | |
 |
|
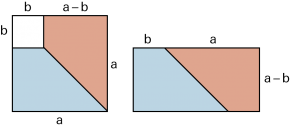
| Formel 3 (a + b) ∙ (a – b) = a2 – b2 | |
| geometrische Deutung: | |
 |
|
Bit - Byte
| Ein Bit ist die kleinstmögliche Informationsmenge, die man auf einem Computer speichern kann. Man kann sich darunter eine Schalterstellung «an» oder «aus», «ja» oder «nein» beziehungsweise «1» oder «0» vorstellen. |
|
8 Bit werden zu 1 Byte gebündelt. 1 Byte ist also eine achtkomponentige Informationsmenge: |
| Speicherkapazitäten eines Sticks, einer Festplatte oder die Grösse eines gespeicherten Musikstücks werden in kB (Kilobyte), MB (Megabyte), GB (Gigabyte) oder TB (Terabyte) angegeben. |
Bruch
|
Ein Bruch kann als Teil eines Ganzen aufgefasst werden («Bruchteil»). |
|||
| Darstellung: | |||
 |
|||
| Der Bruchstrich kann als Divisionszeichen interpretiert werden. Wird die Division ausgeführt, wird die Zahl zum «Dezimalbruch»: | |||
 |
|||
|
Ein Bruch mit Zähler 1 heisst «Stammbruch»:
|
|||
|
Siehe auch Dezimalbruch, Prozent und Bruchoperationen |
Bruchgleichung
| Bruchgleichung ist die Bezeichnung für eine Gleichung, bei der die Unbekannte im Nenner eines Bruchs vorkommt. |
Bruchoperationen
| 1 Kürzen und Erweitern | |
|
Zu jedem Bruch gibt es weitere Brüche mit dem gleichen Wert. Man erhält sie durch kürzen und erweitern. |
|
 |
 |
| Brüche kann man durch Erweitern gleichnamig (gleich-nennrig) machen. | |
| 2 Addition und Subtraktion | |
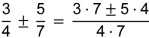 |
|
| 3 Multiplikation | |
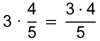 |
|
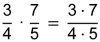 |
|
|
Beachte: |
|
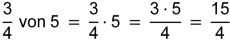 |
|
| 4 Division | |
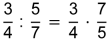 |
|
|
Regel: «Bruch 1 mal Kehrwert von Bruch 2» |
|