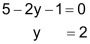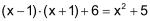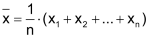Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Abschreibung
|
Ein Gerät oder Fahrzeug verliert jedes Jahr an Wert. In der Buchhaltung ist es üblich, diesen Wertverlust pro Jahr mit einem konstanten Prozentsatz zu verbuchen. Man nennt dies «Abschreibung». Mathematisch gesehen ist die Abschreibung eine exponentielle Abnahme des (Buch-)Werts. |
| siehe auch radioaktiver Zerfall |
absolute Häufigkeit
|
siehe Häufigkeit |
absoluter Fehler
|
Bei einem Messresultat ohne Fehlerangabe gilt die letzte Stelle als gerundet: |
| Günstig ist die Angabe des Messresultats mit dem absoluten Fehler: (64,3 ± 0,2) mm. |
| siehe relativer Fehler und gültige Ziffern |
Abstand
| • | Der Abstand zweier Punkte P und Q ist die Länge der kürzesten Verbindung zwischen ihnen. Man spricht auch von der «Distanz», der «Entfernung» der beiden Punkte oder von der «Länge der Strecke» von P nach Q. |
| • | Der Abstand zwischen einem Punkt und einer Geraden ist die Länge des Lots vom Punkt auf die Gerade. |
| • | Der Abstand zweier Parallelen ist die Länge eines gemeinsamen Lots. (vgl. auch Streifenbreite). |
Achse
| Der Ausdruck wird in verschiedenen Zusammenhängen gebraucht: | |
| 1 | Im (ebenen) Koordinatensystem teilen x- und y-Achse die Ebene in vier Teilgebiete ein, sodass die Lage jedes Punktes durch zwei Zahlen festgelegt ist (siehe Koordinaten). |
| 2 |
Bei einer Geradenspiegelung in der Ebene oder bei der Symmetrieachse einer Figur spricht man kurz von «Achse» (siehe Achsenspiegelung). |
| 3 |
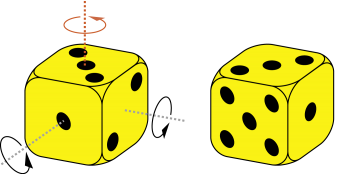
Die Drehung eines Objektes im Raum wird festgelegt durch eine Drehachse und den zugehörigen Drehwinkel. Wird zum Beispiel der linke Würfel in der Abbildung unten um 90° um die vertikale Achse gedreht, ergibt sich die Lage, wie sie in der Abbildung rechts wiedergegeben ist. |
 |
|
Achsenspiegelung
 |
||
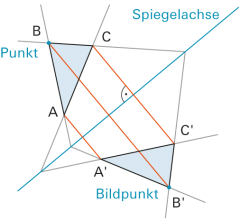
| 1 | Die Achsenspiegelung ist eine Kongruenzabbildung. | |
| • | Die Spiegelachse ist Mittelsenkrechte der Verbindungsstrecke zwischen Punkt und Bildpunkt. | |
| • | Original- und Bildgerade schneiden sich auf der Spiegelachse. | |
| • | Das Bild einer Achsen-Parallelen ist wieder parallel zur Achse | |
| Wird ein ebenes Vieleck an einer Geraden (Spiegelachse) gespiegelt, so hat das Bild den entgegengesetzten Drehsinn. Man spricht hier auch von «entgegengesetzter Orientierung». | ||
| Die Achsenspiegelung wird auch «Geradenspiegelung» genannt. | ||
 |
||
| 2 | Eine Figur heisst achsensymmetrisch, wenn sie beim Falten längs einer bestimmten Geraden mit sich zur Deckung gebracht werden kann. Diese Achse heisst «Symmetrieachse» oder «Spiegelachse». | |
| Eine achsensymmetrische Figur kann auch durch Spiegeln erzeugt werden. | ||
Achsensymmetrie
|
siehe Achsenspiegelung |
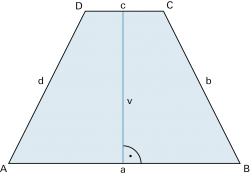
Achsentrapez
Addition
|
Die Addition ist eine Operation erster Ordnung. |
||
|
Eine Summe ist … |
||
| a) | das Ergebnis einer Addition: | |
| 15 + 8 = 23 2a + 3a = 5a | ||
| oder | ||
| b) | der (nicht ausgerechnete) Term mit dem Pluszeichen als Hauptzeichen: | |
 |
||
|
Für die Addition gelten das Assoziativ- und das Kommutativ-Gesetz. |
||
|
Die Umkehroperation der Addition ist die Subtraktion. |
||
| 12 + 7 = 19 ⇔ 19 - 7 = 12 | ||
| Siehe auch Rechengesetze und Bruchoperationen |
Additionsverfahren
| Verfahren zur algebraischen Lösung eines linearen Gleichungssystemes. | |
| Gegeben seien zwei Gleichungen: | 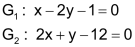 |
| Schritt 1 Gleichung G2 so umformen, dass bei der Addition G1 ⊕ G2 das y «wegfällt» (im Beispiel durch Multiplikation mit 2). |
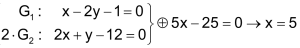 |
| Schritt 2 Ergebnis in Gleichung G1 einsetzen. |
|
|
siehe auch Einsetzungsverfahren und Gleichsetzungsverfahren |
|
ähnlich
Mathematisches Zeichen dafür ist die Wellenlinie: A ∼ B. |
| Ähnliche Figuren kann man durch zentrische Streckung erzeugen. |
Ähnlichkeitsabbildung
|
Haben bei einer Abbildung Original und Bildfigur die gleiche Form, so spricht man von «Ähnlichkeitsabbildung». |
|
Beispiel: |
| Ein Kopierer führt beim Vergrössern oder Verkleinern eine Ähnlichkeitsabbildung aus. |
|
Wichtigste Ähnlichkeitsabbildung ist die Zentrische Streckung. |
Algorithmus [ zurück ]
| Ein Algorithmus ist eine Folge von Anweisungen, nach der eine Berechnung ausgeführt oder eine Ordnung hergestellt wird. Man könnte auch von einer «Programmiervorschrift» reden, die es erlaubt, einen Prozess an eine Maschine auszulagern. | |
| Beispiele | |
|
♦ ♦ ♦ ♦ |
die schriftlichen Rechenverfahren ggT-Bestimmung Heron-Verfahren zur Bestimmung der Quadratwurzel einer Zahl Sortieren einer Namensliste nach Alphabet oder von Zahlen nach ihrer Grösse |
allgemeingültig
|
Wird eine Gleichung oder eine Ungleichung (jeweils mit einer Unbekannten) durch jede Zahl erfüllt, so spricht man von einer «allgemeingültigen Gleichung» bzw. von einer «allgemeingültigen Ungleichung». |
|
Beispiel
|
Altersquotient
|
Der Altersquotient ist definiert als Verhältnis |
 |
| der Wohnbevölkerung. |
äquivalent
| siehe gleichwertig |
Äquivalenzumformung
| Eine Operation, welche eine Gleichung in eine andere Gleichung mit denselben Lösungen überführt, heisst «Äquivalenzumformung» – die beiden Gleichungen nennt man auch «äquivalent». | |
| Äquivalenzumformungen sind … | |
| • | auf beiden Seiten der Gleichung denselben Term addieren oder subtrahieren |
| • | beide Seiten der Gleichung mit demselben Term multiplizieren oder durch denselben Term dividieren, wobei der Term die Unbekannte nicht enthalten darf |
| • | ordnen und zusammenfassen auf der einen oder andern Seite des Gleichheitszeichens |
archimedische Körper
|
Archimedische Körper sind Polyeder, deren Oberfläche sich aus zwei oder mehr verschiedenen Typen regelmässiger Vielecke zusammensetzt. Dabei muss an jeder Ecke die gleiche Konfiguration vorhanden sein. |
|
Zwei Beispiele |
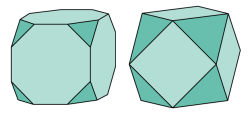 |
| siehe auch platonische Körper |
archimedisches Parkett
| Siehe reguläres Parkett |
arithmetisches Mittel
|
Das arithmetisches Mittel von n Werten wird wie folgt berechnet: |
|
|
Beispiel Das arithmetische Mittel beträgt |
|
|
Oft spricht man auch einfach von «Durchschnitt». |
|
| siehe auch Median und geometrisches Mittel |
Assoziativgesetz
| Siehe Rechengesetze |
ausklammern
| Eine Technik zum Faktorisieren von Summen: Steckt in allen Summanden der Summe ein gemeinsamer Faktor, so lässt sich die Summe als Produkt schreiben. |
|
| Beispiel | |
| 12ab² – 2bc + 6ab³c = 2b · (6ab – c + 3ab²c) | |
ausmultiplizieren
|
Aus einem Produkt gemäss Distributivgesetz eine Summe herstellen. Der umgekehrte Vorgang heisst Ausklammern. |
| Siehe faktorisieren |