Lexikon
Das Lexikon erläutert die mathematischen Begriffe aus allen Jahrgangsbänden.
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
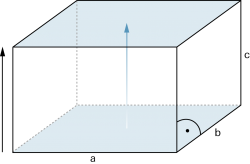
Quader
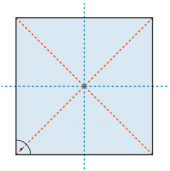
Quadrat
 |
|
| Das Quadrat ist das regelmässigste Viereck. | |
|
• |
Es besitzt vier Symmetrieachsen. |
quadratische Ergänzung
| Zum Lösen einer quadratischen Gleichung der Form x2 + p · x + q = 0 bringt man diese in folgende, leicht lösbare Form: (x + r)2 = s |
|
 |
| Beispiel | |||
|
x2 + 10 · x – 20 |
= = = = = = = |
0 20 20 45 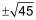 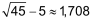 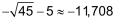 |
quadratische Funktion
|
Eine Funktion mit der Gleichung |
|
| Diese Funktion beschreibt eine (quadratische) Parabel. ♦ Für a > 0 ist die Parabel nach oben geöffnet, für a < 0 nach unten.♦ Ist |a| > 1, dann ist die Parabel «schlank». ♦ Für 0 < |a| < 1 ist die Parabel «ausladend». |
|
|
Man kann diese Vorschrift umformen zur Scheitelpunktsform: |
|
 |
|
|
In dieser Darstellung ist der Scheitelpunkt ist jeweils der tiefste oder der höchste Punkt der Parabel («Minimum» bzw. «Maximum»). |
quadratische Gleichung
|
Eine quadratische Gleichung hat allgemein die Form |
|
Durch Division der allgemeinen quadratischen Gleichung durch a erhält man die «Normalform»: |
| Grafisch ist das leicht einzusehen: |
|
Die Parabel mit der Gleichung |
|
Beim Lösen der Gleichung hilft die quadratische Ergänzung. |
|
Wenn der Ausdruck D = p2 – 4q > 0 ist, hat die Gleichung zwei Lösungen, |
| siehe auch quadratische Funktion |
quadratisches Wachstum
|
Eine Grösse y kann in Abhängigkeit von einer andern Grösse x nicht nur linear oder exponentiell, sondern auch zum Beispiel «quadratisch» (mit x2) oder mit der dritten Potenz (mit x3) wachsen. |
|
Beispiel |
Quadratwurzel
|
Die positive Lösung der Gleichung x2 = a (für a > 0) ist x = «Quadratwurzel aus a». Geschrieben wird die Quadratwurzel aus a als In der Schule wird statt «Quadratwurzel» oft einfach «Wurzel» gesagt. Statt «Quadratwurzel aus a» sagt man «Wurzel a». |
|
|
In den meisten Fälllen ist |
|
| Beispiel | |
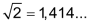 |
|
|
Siehe auch Wurzel, Potenzgesetze |
|
Quersumme
|
Die Summe der Ziffern einer Zahl heisst «Quersumme». |
|
Beispiel |
| Die Teilbarkeit einer Zahl durch 3 oder durch 9 lässt sich leicht über die Quersumme ermitteln. |
Quotient
|
Siehe Division, Rechengesetze und Bruchoperationen |


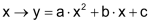
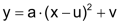
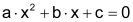
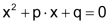
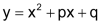
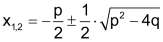
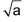 .
.