Lexikon
- abhängige Variable
- Abschreibung
- absolute Häufigkeit
- absoluter Fehler
- Abstand
- Abwicklung
- Achse
- Achsenspiegelung
- Achsensymmetrie
- Achsentrapez
- addieren
- Addition
- Additionsverfahren
- ähnlich
- Ähnlichkeitsabbildung
- Algorithmus
- allgemeingültig
- Altersquotient
- äquivalent
- Äquivalenzumformung
- archimedische Körper
- archimedisches Parkett
- arithmetisches Mittel
- Assoziativgesetz
- ausklammern
- ausmultiplizieren
- ganze Zahlen
- Geburtenüberschuss
- Geburtenüberschussrate
- geometrisches Mittel
- Geradengleichung
- Geradenspiegelung
- Geschwindigkeit
- ggT
- gleichnamig
- gleichseitiges Dreieck
- Gleichsetzungsverfahren
- Gleichung
- gleichwertig
- Grafik
- grafische Darstellung
- Graph
- griechisches Alphabet
- Grössen
- Grundmenge
- Grundoperationen
- gültige Ziffern
- Karat
- kartesisch
- Kathete
- Kathetensatz
- Kegel
- Kegelstumpf
- Kehrbruch
- Kehrwert
- kgV
- kilo-
- Klammerregeln
- Kombinatorik
- Komma
- Kommutativgesetz
- konformer Zinssatz
- kongruent
- Kongruenzabbildung
- Kongruenzsätze
- konvex
- Koordinaten
- Koordinatensystem
- Koordinatensystem, dreidi.. +
- Kreisdiagramm
- Kreisfläche
- Kreissektor
- Kreistangente
- Kreisteile
- Kreisumfang
- Kreiswinkelsätze
- Kreiszahl π
- Kugel
- kürzen
- Parabel
- parallel
- Parallelogramm
- Parameter
- parkettieren
- Penrose-Parkett
- Peripheriewinkel
- Permutation
- Pi
- platonische Körper
- platonisches Parkett
- Polyeder
- Polygon
- Potenz
- Potenzgesetze
- Primfaktorzerlegung
- Primzahl
- Primzahlzwillinge
- Prinzip von Cavalieri
- Prisma
- Produkt
- Projektionen
- Promille
- proportional
- Prozent
- Punkt vor Strich
- Punktoperation
- Punktspiegelung
- Punktsymmetrie
- Pyramide
- Pyramidenstumpf
- Pythagoras-Satz
- Satz des Pythagoras
- Satz des Thales
- Säulendiagramm
- Scheitelpunkt
- Scheitelpunktsform
- Scheitelwinkel
- Schiebung
- Schrägbild
- Schwerlinie
- Schwerpunkt
- Segment
- Sehne
- Sehnenviereck
- Seitenhalbierende im Drei.. +
- Seitenmittendreieck
- Sekante
- Sektor
- senkrecht
- SI-Einheiten
- Stabdiagramm
- Stammbruch
- Statistik
- Steigung
- Stellenwert
- Stichprobe
- Strahlensätze
- Streckenprofil
- Streckenteilung
- Streckfaktor
- Streifenbreite
- Strichoperation
- Stufenwinkel
- subtrahieren
- Subtraktion
- Summand
- Summe
- Symmetrieachse
- Symmetriezentrum
Überschlag
| Um das Resultat einer Rechnung im Kopf näherungsweise zu berechnen, vereinfacht man einzelne Bestandteile so, dass dies leichter möglich ist: | |
| Gefragt ist nicht ein «genaues Resultat», sondern eine sinnvolle, zweckmässige Genauigkeit. Das Ganze heisst dann «Überschlag» oder «Überschlagsrechnung». | |
|
Routinemässig wird mit gerundeten Zahlen überschlagen: |
|
|
• |
4'635 + 1'312 als 5'000 + 1'000 oder als 4'600 + 1'300 ... 3'124 • 243 ≈ 3'000 • 200 oder noch besser 3'000 • 250 |
| In vielen Situationen ist «stures» Runden (im Sinne von Auf- oder Abrunden) keine gute Strategie: | |
| • |
546 • 642 wird durch 500 • 600 zu schlecht geschätzt, besser macht man den einen Faktor kleiner und den anderen grösser, also 500 • 700 oder 600 • 600 |
| • |
8'765 : 26 ≈ 17'000 : 50 oder 34'000 : 100, also etwa 340; hier führt auch 9'000 : 30 auf einen guten Wert. |
| • | 237 • 16'398 ≈ 50 • 8'000 oder 1'000 • 4'000 (Verdoppeln und Halbieren als Strategie) |
| Durch Überschlag veränderte Zahlen müssen auch nicht unbedingt einfacher sein, es muss bloss «besser gehen» | |
| • | 100 : 15 ist etwa 105 : 15 |
| • |
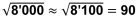 |
| Beim Rechnen mit Brüchen ist man gut beraten, wenn man einen Bruch durch einen einfacheren ersetzt: | |
| • |
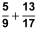 ist etwa ist etwa 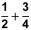 |
| oder man geht über zu Dezimalbrüchen und schätzt dann: | |
| • | 0,55 + 0,78 ≈ 0,6 + 0,7 bzw. ≈ 0,5 + 0,8 |
Umfang
|
Unter «Umfang» versteht man die Länge des Randes einer geschlossenen Figur. |
||
|
Beispiele: |
||
| Rechteck Kreis |
u = 2 · (a + b) u = 2π · r |
|
umgekehrt proportional
|
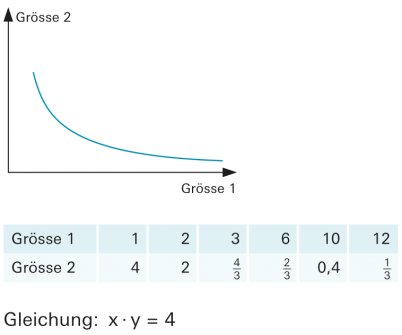
Ist das Produkt zweier einander zugeordneter Grössen x und y immer gleich gross, so spricht man von einer «umgekehrt proportionalen» Zuordnung (oft auch «indirekt proportional» genannt). |
|
Für umgekehrt proportionale Zuordnungen gilt: Das Verdoppeln der einen Grösse bewirkt das Halbieren der anderen Grösse. |
|
Die Darstellung im kartesischen Koordinatensystem ergibt eine Hyperbel. |
 |
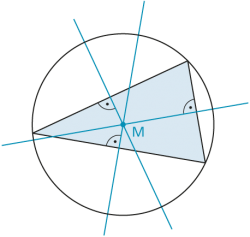
Umkreis
|
|
|
|
Jedes Dreieck hat einen Umkreis. Sein Zentrum ist der Schnittpunkt der Mittelsenkrechten. |
|
|
|
|
| Vielecke mit mehr als drei Ecken haben im Allgemeinen keinen Umkreis. | |
|
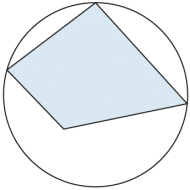
Vierecke, die einen Umkreis haben, heissen Sehnenvierecke. |
|
| Siehe Linien im Dreieck | |
Ungleichung
| Eine «Ungleichung» besteht aus zwei Termen mit einer oder mehreren Variablen, die durch ein Ungleichheitszeichen verbunden sind. | |
|
< |
«kleiner als» |
unlösbar
|
Wird eine Gleichung oder Ungleichung (mit einer Unbekannten) durch keine der zugelassenen Zahlen erfüllt, so spricht man von einer «unlösbaren Gleichung». |
|
Beispiel |
Ursprung
|
Mit «Ursprung» wird der Schnittpunkt der Achsen im Koordinatensystem bezeichnet. |
|
Die Koordinaten des Ursprungs sind somit in der Ebene (0/0) und im Raum (0/0/0). |